题目内容
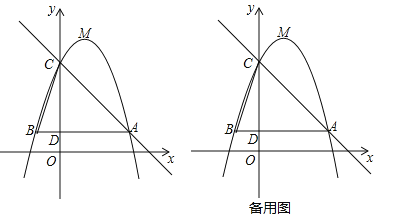
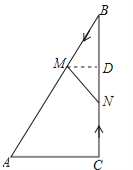
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒![]() cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.

【答案】(1)![]() ;(2)t=
;(2)t=![]() 或t=
或t=![]() ;(3)当t=
;(3)当t=![]() 时,y的值最小.
时,y的值最小.![]() =
=![]() .
.
【解析】(1)∵在Rt△ABC中,∠ACB=90°,AC=5,∠BAC=60°,∴∠B=30°,∴AB=2AC=10,BC=![]() .
.
由题意知:BM=2t,CN=![]() ,∴BN=
,∴BN=![]() ,∵BM=BN,∴
,∵BM=BN,∴![]() ,解得:t=
,解得:t=![]() =
=![]() .
.
(2)分两种情况:①当△MBN∽△ABC时,则![]() ,即
,即![]() ,解得:t=
,解得:t=![]() .
.
②当△NBM∽△ABC时,则![]() ,即
,即![]() ,解得:t=
,解得:t=![]() .
.
综上所述:当t=![]() 或t=
或t=![]() 时,△MBN与△ABC相似.
时,△MBN与△ABC相似.
(3)过M作MD⊥BC于点D,则MD∥AC,∴△BMD∽△BAC,∴![]() ,即
,即![]() ,解得:MD=t.
,解得:MD=t.
设四边形ACNM的面积为y,∴y=![]() =
=![]() ,∴根据二次函数的性质可知,当t=
,∴根据二次函数的性质可知,当t=![]() 时,y的值最小.此时,
时,y的值最小.此时,![]() =
=![]() .
.

练习册系列答案
相关题目