题目内容
【题目】在平面直角坐标系中,对于点P(a,b),若点P′的坐标为(![]() ,
,![]() )(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
(1)点P(﹣3,4)的“2关联点”P′的坐标是_______________;
(2)若a、b为正整数,点P的“k关联点”P′的坐标为(3,9),请直接写出k的值及点P的坐标;
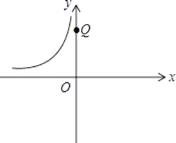
(3)如图,点Q的坐标为(0,2 ),点A在函数![]() 的图象上运动,且点A是点B的“﹣
的图象上运动,且点A是点B的“﹣![]() 关联点”,求线段BQ的最小值.
关联点”,求线段BQ的最小值.
【答案】(1)(-1,-2); (2)![]() , P(1,6)或P(2,3);(3)BQ的最小值为
, P(1,6)或P(2,3);(3)BQ的最小值为![]()
【解析】
(1)根据题中的新定义求出点P(-3,4)的“2关联点”P′的坐标即可;
(2)根据题中的新定义求出a与b的关系式即可;
(3)设点B的坐标为(m,n),从而表示出点A的坐标(m+![]() ,-
,-![]() m+n),由点A在函数
m+n),由点A在函数![]() 的图象上可得到m、n之间的关系n=4+
的图象上可得到m、n之间的关系n=4+![]() m.然后将BQ2用m的代数式表示,根据二次函数的最值性,求出BQ最小值.
m.然后将BQ2用m的代数式表示,根据二次函数的最值性,求出BQ最小值.
(1)∵x=-3+![]() =-1,y=2×(-3)+4=-2,
=-1,y=2×(-3)+4=-2,
∴P′(-1,-2);
(2)设P(a,b),则P′(![]() ,ka+b)
,ka+b)
∴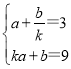 ,
,
∴k=3,
∴3a+b=9.
∵a、b为正整数
∴P′(1,6)、(2,3);
(3)设点B的坐标为(m,n),
∵点A是点B的“﹣![]() 关联点”,
关联点”,
∴点A的坐标为(m+![]() ,-
,-![]() m+n),
m+n),
∵点A在函数![]() 的图象上,
的图象上,
∴(m+![]() )(-
)(-![]() m+n)=-8
m+n)=-8![]() ,且m+
,且m+![]() <0.
<0.
整理得:(m+![]() )2=8.
)2=8.
∵m+![]() <0,
<0,
∴m+![]() =-2
=-2![]() .
.
∴n=4+![]() m.
m.
∴点B的坐标为(m,4+![]() m).
m).
过点B作BH⊥OQ,垂足为H,如图所示.

∵点Q的坐标为(0,2),
∴QH2=(2-4-![]() m)2=(2+
m)2=(2+![]() m)2,BH2=m2.
m)2,BH2=m2.
∴BQ2=BH2+QH2
=m2+(2+![]() m)2
m)2
=3m2+4![]() m+4
m+4
=3(m+![]() )2+
)2+![]()
∵3>0,
∴当m=-![]() 时,BQ2最小,即BQ2 =
时,BQ2最小,即BQ2 =![]() .
.
∴BQ=![]() .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案