Question

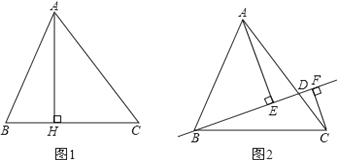
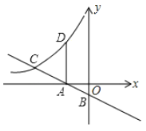
【题目】定义：圆中有公共端点的两条弦组成的折线称为圆的一条折弦．阿基米德折弦定理：如图1，AB和BC组成圆的折弦，AB＞BC，M是弧ABC的中点，MF⊥AB于F，则AF＝FB+BC．

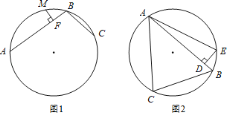
如图2，△ABC中，∠ABC＝60°，AB＝8，BC＝6，D是AB上一点，BD＝1，作DE⊥AB交△ABC的外接圆于E，连接EA，则∠EAC＝_____°．

Answer 1

【答案】60°．

【解析】

连接OA、OC、OE，由已知条件，根据阿基米德折弦定理，可得到点E为弧ABC的中点，即,进而推得∠AOE＝∠COE，已知∠ABC＝60°，则∠AOC＝2∠ABC＝2×60°＝120°，可知∠AOE＝∠COE＝120°，故∠CAE＝∠COE＝60°.

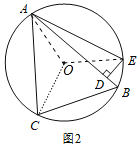
解：如图2，连接OA、OC、OE，

∵AB＝8，BC＝6，BD＝1，

∴AD＝7，BD+BC＝7，

∴AD＝BD+BC，

而ED⊥AB，

∴点E为弧ABC的中点，即，

∴∠AOE＝∠COE，

∵∠AOC＝2∠ABC＝2×60°＝120°，

∴∠AOE＝∠COE＝120°，

∴∠CAE＝∠COE＝60°．

故答案为60°．