题目内容
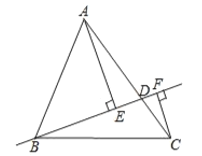
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
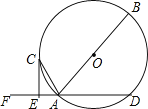
【答案】(1)证明见解析;(2)2.5.
【解析】
试题(1)证明:连接CO,证得∠OCA=∠CAE,由平行线的判定得到OC∥FD,再证得OC⊥CE,即可证得结论;
(2)证明:连接BC,由圆周角定理得到∠BCA=90°,再证得△ABC∽△ACE,根据相似三角形的性质即可证得结论.
试题解析:(1)证明:连接CO,∵OA=OC,∴∠OCA=∠OAC,∵AC平分∠FAB,∴∠OCA=∠CAE,∴OC∥FD,∵CE⊥DF,∴OC⊥CE,∴CE是⊙O的切线;
(2)证明:连接BC,在Rt△ACE中,AC=![]() =
=![]() =
=![]() ,∵AB是⊙O的直径,∴∠BCA=90°,∴∠BCA=∠CEA,∵∠CAE=∠CAB,∴△ABC∽△ACE,∴
,∵AB是⊙O的直径,∴∠BCA=90°,∴∠BCA=∠CEA,∵∠CAE=∠CAB,∴△ABC∽△ACE,∴![]() ,∴
,∴![]() ,∴AB=5,∴AO=2.5,即⊙O的半径为2.5.
,∴AB=5,∴AO=2.5,即⊙O的半径为2.5.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目