Question

【题目】提出问题

若矩形的面积为9，则该矩形的周长有无最大值或最小值？若有，最大（小）值是多少？

分析问题

若设该矩形的长为，则矩形的宽为，若周长为，则与的函数关系式为，问题就转化为研究该函数的最值问题．

解决问题

“数学兴趣小组”对函数的最值问题进行了探究，探究过程如下：

（1）填写下表，并用描点法在坐标系中画出函数的图象，

		1	2	3	4	5
		20		12

其中__________；

（2）观察该函数的图象，当__________时，函数有最__________值（填“大”或“小”），其最值是__________；

（3）在求二次函数的最大（小）值时，我们可以通过配方的形式将函数表达式变为顶点式求出最值，同样函数也可以通过配方求最值：

当时，即时，．

请类比上面配方法，验证我们对该函数的最值的猜想．

Answer 1

【答案】（1）13，详见解析；（2）3，小，12；（3）当时，有最小值，最小值为12．

【解析】

（1）分别把表中x的值代入所得函数关系式可求m的值，并画出函数图象即可；
（2）根据（1）中函数图象的顶点坐标直接得出结论即可；
（3）利用配方法把原式化为平方的形式，再求出其最值即可．

（1）当x=2时， ；

画出函数图像如解图：

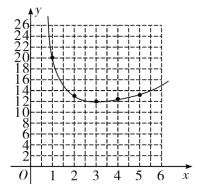
（2）由函数图象可知，其顶点坐标为（3，12），故当x=3时函数有最小值，最小值为12，

故答案为：3，小，12；

（3）

，

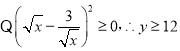当时，有最小值，最小值为12，

即当时，有最小值，最小值为12．