��Ŀ����
����Ŀ������������⣺
��1���Ķ����⣺
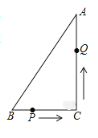
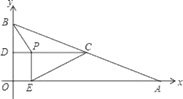
��ͼ1����![]() �У���
����![]() ��
��![]() ����
����![]() ���ϵ�����
���ϵ�����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
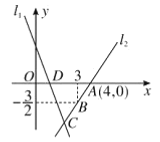
�����������������·������ӳ�![]() ����
����![]() ʹ
ʹ![]() ��������
��������![]() ����
����![]() ����
����![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ����
����![]() ��
��![]() ��
��![]() ������
������![]() �У��������������ߵĹ�ϵ�����ж�.����
�У��������������ߵĹ�ϵ�����ж�.����![]() ��ȡֵ��Χ��______.
��ȡֵ��Χ��______.
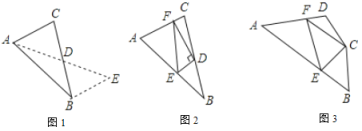
��2����������
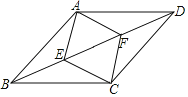
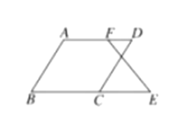
��ͼ2����![]() �У�
��![]() ��
��![]() ���ϵ��е㣬
���ϵ��е㣬![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ����֤��
����֤��![]() .
.
��3��������չ��
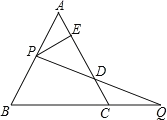
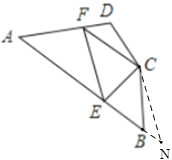
��ͼ3�����ı���![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() Ϊ������һ��
Ϊ������һ��![]() �ǣ��ǵ����߷ֱ�
�ǣ��ǵ����߷ֱ�![]() ��
��![]() ��
��![]() ��
��![]() ���㣬����
���㣬����![]() ��̽���߶�
��̽���߶�![]() ��
��![]() ��
��![]() ֮���������ϵ��������֤��.
֮���������ϵ��������֤��.
���𰸡���1��2<AD<8����2��֤������������3��EF=BE+DF��֤��������.
��������
��1������SAS��֤����ADC����EDB���ɵ�BE=AC=6���������������߹�ϵ���ɵô𰸣���2���ӳ�FD����M��ʹDM=DF������BM��EM��ͬ��1���ɵ�CF=BM�����ݴ�ֱƽ�������ʿɵ�EF=EM���������������߹�ϵ���ɵô𰸣���3���ӳ�AB��N��ʹBN=DF������CN���ɵá�NBC=��D������SAS֤����NBC�ա�FDC���ó�CN=CF����NCB=��FCD�����ýǵĺͲ��ϵ�ɵá�ECN=70��=��ECF������SAS֤����NCE�ա�FCE���ó�EN=EF�����ɵó����ۣ�
��1����CD=BD����ADC=��EDB��AD=DE��
����ADC����EDB��
��BE=AC=6��
����ABE��AB-BE<AE<AB+BE����10-6<2AD<10+6��
��2<AD<8��
�ʴ�Ϊ��2<AD<8
��2����ͼ���ӳ�FD����M��ʹDM=DF������BM��EM��
ͬ��1����CF=BM��
��FD=MD��DE��DF��
��EF=EM��
����BEM��BE+BM>EM��
��BE+CF>EF.
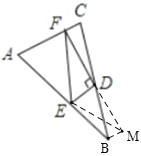
��3��EF=BE+DF��֤�����£�
��ͼ���ӳ�AB��N��ʹBN=DF������CN��
�ߡ�D+��ABC=180������ABC+��NBC=180����
���D=��NBC��
����NBC����FDC��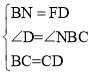 ��
��
����NBC�ա�FDC��
��CN=CF����NCB=��FCD��
�ߡ�ECF=70������BCD=140����
���FCD+��ECB=70����
���NCB+��ECB=70��������ECN=70��=��ECF��
����FCE����NCE��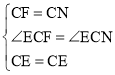 ��
��
����NCE�ա�FCE��
��EF=EN=BE+BN=BE+DF.

 ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�