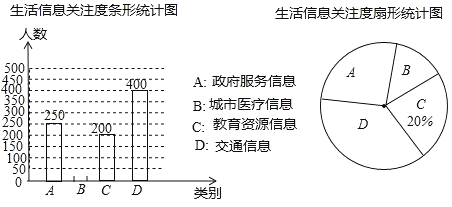
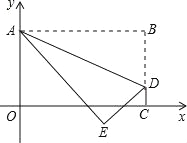
题目内容
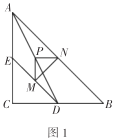
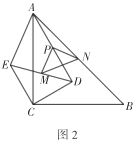
【题目】如图,在四边形 ABCD 中,AD ∥ BC ,∠BCD=90° ,∠ABC=45° ,AD=CD ,CE 平分 ∠ ACB 交 AB 于点 E ,在 BC 上截取 BF=AE ,连接 AF 交 CE 于点 G ,连接 DG 交 AC 于点 H ,过点 A 作 AN ⊥ BC ,垂足为 N , AN 交 CE 于点 M .则下列结论:① CM=AF ; ② CE ⊥ AF ; ③△ ABF ∽△ DAH ;④ GD 平分 ∠ AGC ,其中正确的序号是 ________ .
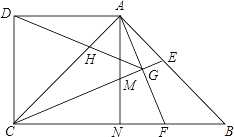
【答案】①②③④
【解析】
结论 ① 正确,证明 △ ACM ≌△ ABF 即可;结论 ② 正确,由 △ ACM ≌△ ABF 得出 ∠ 2= ∠ 4 ,进而得 ∠ 4+∠ 6=90° ,即 CE ⊥ AF ,结论 ③ 正确,证法一:利用四点共圆;证法二:利用三角形全等;结论 ④ 正确,证法一:利用四点共圆,证法二:利用三角形全等.
解:
![]()
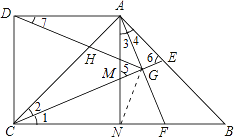
⑴ 结论 ① 正确.理由如下:
∵∠1=∠2 , ∠1+∠CMN=90° ,∠2+∠6=90° ,
∴∠6=∠CMN ,![]()
又 ∵∠5=∠CMN ,
∴∠5= ∠6 ,
∴ AM=AE=BF .
∵∠BCD=90° ,AN⊥BC,垂足为 N,
∴AN∥CD,
∵AD∥BC∴四边形ADCN是平行四边形,
∵∠BCD=90°,AD=CD
∴ ADCN 为正方形,△ ABC为等腰直角三角形,
∴ AB=AC .
在△ ACM与△ ABF 中,
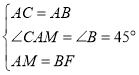 ,
,
∴△ACM ≌△ABF(SAS),
∴ CM=AF ;
⑵ 结论②正确.理由如下:
∵△ACM ≌△ABF ,
∴∠2=∠4 ,
∵∠2+∠6=90° ,
∴∠4+∠6=90° ,
∴ CE⊥AF ;
⑶ 结论③正确.理由如下:
证法一: ∵CE⊥AF ,
∴∠ADC+∠AGC=180° ,
∴ A 、D 、C 、G 四点共圆,
∴∠7=∠2 ,
∵∠2=∠4 ,
∴∠7=∠4 ,
又 ∵∠DAH=∠B=45° ,
∴△ABF∽△DAH ;
证法二: ∵ CE⊥AF, ∠1=∠2 ,
∴△ACF为等腰三角形,AC=CF,点G为AF中点.
在 Rt△ANF中,点G为斜边AF中点,
∴ NG=AG ,
∴∠MNG=∠3 ,
∴∠DAG=∠CNG .
在△ADG与△NCG 中,
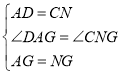 ,
,
∴△ADG≌△NCG ( SAS),
∴∠7=∠1 ,
又 ∵∠1=∠2=∠4 ,
∴∠7=∠4 ,
又 ∵∠DAH=∠B=45° ,
∴△ABF∽△DAH ;
⑷ 结论④正确.理由如下:
证法一: ∵ A、D、C、G 四点共圆,
∴∠DGC=∠DAC=45° , ∠DGA=∠DCA=45° ,
∴∠DGC=∠DGA ,即GD平分∠AGC .
证法二: ∵ AM=AE ,CE⊥AF ,
∴∠3=∠4 ,又 ∠2=∠4 , ∴∠3=∠2
则 ∠CGN=180°-∠ 1- 90°-∠MNG=180°﹣∠1﹣90°﹣∠3=90°-∠1-∠2=45° .
∵△ADG ≌△NCG ,
∴∠DGA=∠CGN=45°=![]() ∠AGC ,
∠AGC ,
∴ GD平分∠AGC .
综上所述,正确的结论是:①②③④,共 4 个.
故答案为: ①②③④

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】提出问题
若矩形的面积为9,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的长为![]() ,则矩形的宽为
,则矩形的宽为![]() ,若周长为
,若周长为![]() ,则
,则![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,问题就转化为研究该函数的最值问题.
,问题就转化为研究该函数的最值问题.
解决问题
“数学兴趣小组”对函数![]() 的最值问题进行了探究,探究过程如下:
的最值问题进行了探究,探究过程如下:
(1)填写下表,并用描点法在坐标系中画出函数![]() 的图象,
的图象,
|
| 1 | 2 | 3 | 4 | 5 |
|
|
| 20 |
| 12 |
|
|
|
其中![]() __________;
__________;
(2)观察该函数的图象,当![]() __________时,函数
__________时,函数![]() 有最__________值(填“大”或“小”),其最值是__________;
有最__________值(填“大”或“小”),其最值是__________;
(3)在求二次函数![]() 的最大(小)值时,我们可以通过配方的形式将函数表达式变为顶点式求出最值,同样函数
的最大(小)值时,我们可以通过配方的形式将函数表达式变为顶点式求出最值,同样函数![]() 也可以通过配方求最值:
也可以通过配方求最值:
![]()
![]()
![]() 当
当![]() 时,即
时,即![]() 时,
时,![]() .
.
请类比上面配方法,验证我们对该函数![]() 的最值的猜想.
的最值的猜想.