题目内容
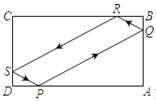
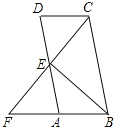
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一点,且
边上一点,且![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,当
,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长为__________.
的长为__________.
【答案】3或![]()
【解析】
①当BC=CM时,△BCM为等腰三角形,
②当BM=CM时,当△BCM为等腰三角形时,
③当BC=BM=3时,由折叠的性质得,根据等腰三角形的性质和勾股定理即可得到结论.
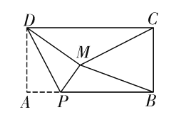
:①如图1,当BC=CM时,△BCM为等腰三角形,
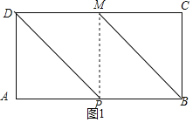
∴点M落在CD边上,如图1,DN=AD=3,
∴四边形APMD是正方形,
∴AP=3,∵AB=CD=6,
∴BP=3;
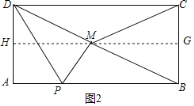
②如图2,当BM=CM时,当△BCM为等腰三角形时,
 ,
,
∴点M落在BC的垂直平分线上,如图2,
过M作BC的垂直平分线交AD于H交BC于G,
∴![]()
∵将△ADP沿DP折叠,点A落在点M处,
∴AD=DM,
∴![]() ,
,
∴∠ADM=60°,
∴∠ADP=∠PDM=30°,
∴![]() ,
,
∴![]() ;
;
③当BC=BM=3时,由折叠的性质得,DM=AD=3,
∴DM+BM=6,而![]() ,
,
∴DM+BM<BD,故这种情况不存在,
综上所述,BP的长为3或![]() ;
;
故答案为:3或![]() .
.

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】提出问题
若矩形的面积为9,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的长为![]() ,则矩形的宽为
,则矩形的宽为![]() ,若周长为
,若周长为![]() ,则
,则![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,问题就转化为研究该函数的最值问题.
,问题就转化为研究该函数的最值问题.
解决问题
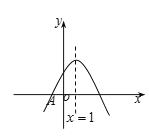
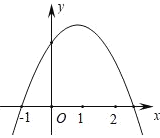
“数学兴趣小组”对函数![]() 的最值问题进行了探究,探究过程如下:
的最值问题进行了探究,探究过程如下:
(1)填写下表,并用描点法在坐标系中画出函数![]() 的图象,
的图象,
|
| 1 | 2 | 3 | 4 | 5 |
|
|
| 20 |
| 12 |
|
|
|
其中![]() __________;
__________;
(2)观察该函数的图象,当![]() __________时,函数
__________时,函数![]() 有最__________值(填“大”或“小”),其最值是__________;
有最__________值(填“大”或“小”),其最值是__________;
(3)在求二次函数![]() 的最大(小)值时,我们可以通过配方的形式将函数表达式变为顶点式求出最值,同样函数
的最大(小)值时,我们可以通过配方的形式将函数表达式变为顶点式求出最值,同样函数![]() 也可以通过配方求最值:
也可以通过配方求最值:
![]()
![]()
![]() 当
当![]() 时,即
时,即![]() 时,
时,![]() .
.
请类比上面配方法,验证我们对该函数![]() 的最值的猜想.
的最值的猜想.