题目内容
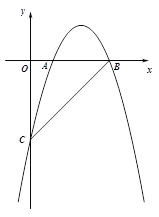
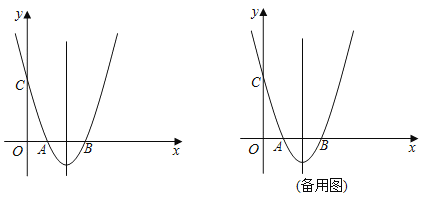
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
(1)求该抛物线的表达式及顶点坐标;
(2)点P为抛物线上一点(不与点A重合),连接PC.当∠PCB=∠ACB时,求点P的坐标;
(3)在(2)的条件下,将抛物线沿平行于y轴的方向向下平移,平移后的抛物线的顶点为点D,点P的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.
【答案】(1)y=x2﹣4x+3,抛物线顶点坐标是(2,﹣1);(2)P(![]() ,
,![]() );(3)抛物线平移的距离为
);(3)抛物线平移的距离为![]() .
.
【解析】
(1)由抛物线的对称性质得到点B的坐标,把点A、B的坐标分别代入抛物线解析式,列出方程组,通过解方程组求得系数的值;根据抛物线解析式求得顶点坐标;
(2)过点P作PN⊥x轴于N,过点C作CM⊥PN,交NP的延长线于点M,构造矩形COMN和直角三角形,利用锐角三角函数的定义求得![]() ,故设PM=a,MC=3a,PN=3-a.易得P(3a,3-a),由二次函数图象上点的坐标特征列出关于a的方程,通过解方程求得a的值,易得点P的坐标;
,故设PM=a,MC=3a,PN=3-a.易得P(3a,3-a),由二次函数图象上点的坐标特征列出关于a的方程,通过解方程求得a的值,易得点P的坐标;
(3)设抛物线平移的距离为m,得y=(x-2)2-1-m.从而求得D(2,-1-m).过点D作直线EF∥x轴,交y轴于点E,交PQ延长线于点F.易推知∠EOD=∠QDF,则tan∠EOD=tan∠QDF,根据锐角三角函数定义列出关于m的方程,通过解方程求得m的值.
解:(1)∵对称轴为直线x=2,点A的坐标为(1,0),
∴点B的坐标是(3,0).
将A(1,0),B(3,0)分别代入y=x2+bx+c,得
![]() .
.
解得![]() .
.
则该抛物线解析式是:y=x2﹣4x+3.
由y=x2﹣4x+3=(x﹣2)2﹣1知,该抛物线顶点坐标是(2,﹣1);
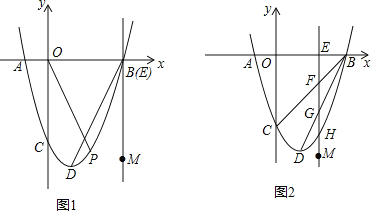
(2)如图1,过点P作PN⊥x轴于N,过点C作CM⊥PN,交NP的延长线于点M,
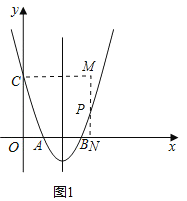
∵∠CON=90°,
∴四边形CONM是矩形.
∴∠CMN=90°,CO=MN、
∴y=x2﹣4x+3,
∴C(0,3).
∵B(3,0),
∴OB=OC=3.
∵∠COB=90°,
∴∠OCB=∠BCM=45°.
又∵∠ACB=∠PCB,
∴∠OCB﹣∠ACB=∠BCM﹣∠PCB,即∠OCA=∠PCM.
∴tan∠OCA=![]() =tan∠PCM.
=tan∠PCM.
∴![]() .
.
故设PM=a,MC=3a,PN=3﹣a.
∴P(3a,3﹣a),
将其代入抛物线解析式y=x2﹣4x+3,得(3a)2﹣4(3﹣a)+3=3﹣a.
解得a1=![]() ,a2=0(舍去).
,a2=0(舍去).
∴P(![]() ,
,![]() ).
).
(3)设抛物线平移的距离为m,得y=(x﹣2)2﹣1﹣m.
∴D(2,﹣1﹣m).
如图2,过点D作直线EF∥x轴,交y轴于点E,交PQ延长线于点F,

∵∠OED=∠QFD=∠ODQ=90°,
∴∠EOD+∠ODE=90°,∠ODE+∠QDP=90°.
∴∠EOD=∠QDF.
∴tan∠EOD=tan∠QDF,
∴![]() .
.
∴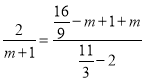 .
.
解得m=![]() .
.
故抛物线平移的距离为![]() .
.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案