ĢāÄæÄŚČŻ
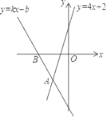
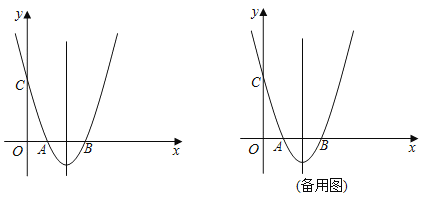
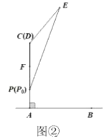
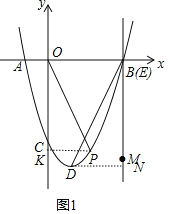
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖÅ×ĪļĻßy£½![]() x2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚµćA£Ø©2£¬0£©£¬µćB£Ø6£¬0£©£¬ÓėyÖį½»ÓŚµćC£¬¶„µćĪŖD£®
x2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚµćA£Ø©2£¬0£©£¬µćB£Ø6£¬0£©£¬ÓėyÖį½»ÓŚµćC£¬¶„µćĪŖD£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µćEŹĒĻ߶ĪABÉĻµÄµć£¬Ö±ĻßEM”ĶxÖį£¬ÉčµćEµÄŗį×ų±źĪŖt£®
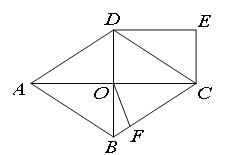
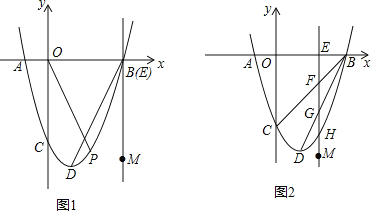
¢Łµ±t£½6Ź±£ØČēĶ¼1£©£¬µćPĪŖxÖįĻĀ·½Å×ĪļĻßÉĻµÄŅ»µć£¬Čō”ĻCOP£½”ĻDBM£¬Ēó“ĖŹ±µćPµÄŗį×ų±ź£»
¢Śµ±2£¼t£¼6Ź±£ØČēĶ¼2£©£¬Ö±ĻßEMÓėĻ߶ĪBC£¬BDŗĶÅ×ĪļĻß·Ö±šĻą½»ÓŚµćF£¬G£¬H£¬ŹŌÖ¤Ć÷Ļ߶ĪEF£¬FG£¬GH×ÜÄÜ×é³ÉµČŃüČż½ĒŠĪ£¬Čē¹ū“ĖµČŃüČż½ĒŠĪµ×½ĒµÄÓąĻŅÖµĪŖ![]() £¬Ēó“ĖµČŃüČż½ĒŠĪµÄĆ껿£®
£¬Ēó“ĖµČŃüČż½ĒŠĪµÄĆ껿£®
”¾“š°ø”æ(1) y£½![]() x2©2x©6£»(2)¢ŁµćPµÄŗį×ų±źĪŖ2
x2©2x©6£»(2)¢ŁµćPµÄŗį×ų±źĪŖ2![]() £¬¢Ś
£¬¢Ś![]() £®
£®
”¾½āĪö”æ
£Ø1£©øł¾ŻÅ×ĪļĻßy£½![]() x2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚA£Ø©2£¬0£©£¬B£Ø6£¬0£©£¬ĄūÓĆ½»µćŹ½æÉČ·¶ØÅ×ĪļĻß½āĪöŹ½£»
x2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚA£Ø©2£¬0£©£¬B£Ø6£¬0£©£¬ĄūÓĆ½»µćŹ½æÉČ·¶ØÅ×ĪļĻß½āĪöŹ½£»
£Ø2£©¢Ł¹żµćD×÷DN”ĶBMÓŚN£¬¹żµćP×÷PK”ĶyÖįÓŚK£¬ĻČĒótan”ĻDBN£¬ŌŁøł¾ŻĢāŅā”ĻCOP=”ĻDBM£¬¼“tan”ĻCOP=tan”ĻDBN£¬æÉĒóµćPµÄŗį×ų±ź£»
¢Ś“ż¶ØĻµŹż·ØĒóµĆ£ŗÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=x-6£¬Ö±ĻßBDµÄ½āĪöŹ½ĪŖy=2x-12£¬±ķŹ¾³öF£¬G£¬HµÄ×ų±ź£¬¼“æÉÖ¤Ć÷£ŗĻ߶ĪEF£¬FG£¬GH×ÜÄÜ×é³ÉµČŃüČż½ĒŠĪ£¬ŌŁ¼ĘĖćÓÉĻ߶ĪEF£¬FG£¬GH×é³ÉµČŃüČż½ĒŠĪµÄĆ껿£®
½ā£ŗ£Ø1£©øł¾ŻÅ×ĪļĻßy£½![]() x2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚA£Ø©2£¬0£©£¬B£Ø6£¬0£©£¬
x2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚA£Ø©2£¬0£©£¬B£Ø6£¬0£©£¬
ÉčÅ×ĪļĻß½āĪöŹ½ĪŖy£½![]() £Øx+2£©£Øx©6£©£¬
£Øx+2£©£Øx©6£©£¬
¼“y£½![]() x2©2x©6£»
x2©2x©6£»
£Ø2£©¢ŁČēĶ¼1£¬¹żµćD×÷DN”ĶBMÓŚN£¬¹żµćP×÷PK”ĶyÖįÓŚK£¬
Ōņ”ĻBND£½”ĻOCP£½90”ć
”ßy£½![]() £Øx©2£©2©8
£Øx©2£©2©8
”ąD£Ø2£¬©8£©£¬B£Ø6£¬0£©£¬N£Ø6£¬©8£©£¬
”ątan”ĻDBN£½![]() £½
£½![]() £½
£½![]() £¬
£¬
”ß”ĻCOP£½”ĻDBM£¬
”ątan”ĻCOP£½tan”ĻDBN£½![]() £¬
£¬
ÉčP£Øm£¬![]() ©2m©6£©£¬ŌņKP£½m£¬OK£½©£Ø
©2m©6£©£¬ŌņKP£½m£¬OK£½©£Ø![]() ©2m©6£©
©2m©6£©
”ą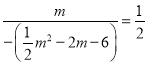 £¬½āµĆ£ŗm1£½©2
£¬½āµĆ£ŗm1£½©2![]() £Ø²»·ūŗĻĢāŅā£¬ÉįČ„£©£¬m2£½2
£Ø²»·ūŗĻĢāŅā£¬ÉįČ„£©£¬m2£½2![]() £¬
£¬
”ąµćPµÄŗį×ų±źĪŖ2![]() £¬
£¬
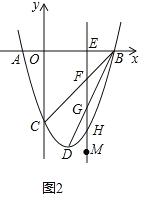
¢ŚČēĶ¼2£¬”ßB£Ø6£¬0£©£¬C£Ø0£¬©6£©£¬D£Ø2£¬©8£©£¬
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy£½x©6£¬Ö±ĻßBDµÄ½āĪöŹ½ĪŖy£½2x©12£¬
”ßE£Øt£¬0£©£¬
”ąF£Øt£¬t©6£©£¬G£Øt£¬2t©12£©£¬H£Øt£¬![]() ©2t©6£©
©2t©6£©
”ąEF£½6©t£¬FG£½t©6©£Ø2t©12£©£½6©t£¬GH£½2t©12©£Ø![]() ©2t©6£©£½©
©2t©6£©£½©![]() +4t©6£¬
+4t©6£¬
”ąEF£½FG
”ßEF+FG£½12©2t£¬EF+FG©GH£½12©2t©£Ø©![]() +4t©6£©£½
+4t©6£©£½![]() ©6t+18£½
©6t+18£½![]() £¬
£¬
”ąµ±2£¼t£¼6Ź±£¬![]() £¾0£¬¼“EF+FG£¾GH
£¾0£¬¼“EF+FG£¾GH
”ąĻ߶ĪEF£¬FG£¬GH×ÜÄÜ×é³ÉµČŃüČż½ĒŠĪ£¬
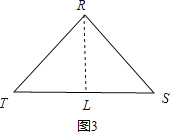
ČēĶ¼3£¬”÷RTSÖŠ£¬ÉčRT£½RS£½6©t£¬TS£½©![]() +4t©6£¬×÷RL”ĶTSÓŚL£¬Ōņ”ĻRLT£½90”ć
+4t©6£¬×÷RL”ĶTSÓŚL£¬Ōņ”ĻRLT£½90”ć
”ßRT£½RS£¬RL”ĶTS
”ąTL£½![]() TS£½©
TS£½©![]() +2t©3
+2t©3
ŅĄĢāŅāÓŠcos”ĻRTS£½![]() £¬¼“
£¬¼“![]() £½
£½![]()
”ą2£Ø6©t£©£½3£Ø©![]() +2t©3£©£¬½āµĆ£ŗt1£½6£Ø²»·ūŗĻĢāŅā£¬ÉįČ„£©£¬t2£½
+2t©3£©£¬½āµĆ£ŗt1£½6£Ø²»·ūŗĻĢāŅā£¬ÉįČ„£©£¬t2£½![]() £¬
£¬
”ąTL£½![]() £¬TS£½
£¬TS£½![]() £¬RT£½
£¬RT£½![]()
”ąRL£½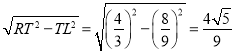
”ąS”÷RTS£½![]() TSRL£½
TSRL£½![]() ”Į
”Į![]() ”Į
”Į![]() £½
£½![]() £®
£®
”ąĻ߶ĪEF£¬FG£¬GH×é³ÉµÄµČŃüČż½ĒŠĪµÄĆ껿ĪŖ£ŗ![]() £®
£®

 Ó„ÅɽĢøØĻĪ½Ó½Ģ²ÄŗÓ±±½ĢÓż³ö°ęÉēĻµĮŠ“š°ø
Ó„ÅɽĢøØĻĪ½Ó½Ģ²ÄŗÓ±±½ĢÓż³ö°ęÉēĻµĮŠ“š°ø ³õÖŠŹīĘŚĻĪ½ÓĻµĮŠ“š°ø
³õÖŠŹīĘŚĻĪ½ÓĻµĮŠ“š°ø”¾ĢāÄæ”æĖę×ÅĪŅ¹ś¾¼ĆÉē»įµÄ·¢Õ¹£¬ČĖĆń¶ŌÓŚĆĄŗĆÉś»īµÄ×·ĒóŌ½Ą“Ō½øߣ®Ä³ÉēĒųĪŖĮĖĮĖ½ā¼ŅĶ„¶ŌÓŚĪĻƽĢÓżµÄĻū·ŃĒÄæö£¬Ė껜³éČ”²æ·Ö¼ŅĶ„£¬¶ŌĆ滧¼ŅĶ„µÄĪĻƽĢӿğĻū·Ń½š¶ī½ųŠŠĪŹ¾ķµ÷Ė£¬øł¾Żµ÷²é½į¹ū»ęÖĘ³ÉĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼±ķ£®
ĒėÄćøł¾ŻĶ³¼ĘĶ¼±ķĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
×ée | ¼ŅĶ„ÄźĪĻƽĢÓżĻū·Ń½š¶īx£ØŌŖ£© | »§Źż |
A | xӆ5000 | 36 |
B | 5000£¼x”Ü10000 | m |
C | 10000£¼x”Ü15000 | 27 |
D | 15000£¼x”Ü20000 | 15 |
E | x£¾20000 | 30 |
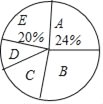
£Ø1£©±¾“Ī±»µ÷ĖµÄ¼ŅĶ„ÓŠ__________»§£¬±ķÖŠ m=__________£»
£Ø2£©±¾“Īµ÷²éŹż¾ŻµÄÖŠĪ»Źż³öĻÖŌŚ__________×飮ÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬D×éĖłŌŚÉČŠĪµÄŌ²ŠÄ½ĒŹĒ__________¶Č£»
£Ø3£©ÕāøöÉēĒųÓŠ2500»§¼ŅĶ„£¬ĒėÄć¹Ą¼Ę¼ŅĶ„ÄźĪĻƽĢÓżĻū·Ń10000ŌŖŅŌÉĻµÄ¼ŅĶ„ÓŠ¶ąÉŁ»§£æ