题目内容
【题目】已知二次函数y＝ax2+bx+c的图象过点A（1，2），B（3，2），C（5，7）．若点M（﹣2，y1），N（﹣1，y2），K（8，y3）也在二次函数y＝ax2+bx+c的图象上，则y1，y2，y3从小到大的关系是_____
【答案】y2＜y1＜y3
【解析】
将A（1，2），B（3，2），C（5，7）代入二次函数中，求出二次函数．然后确定二次函数抛物线对称轴，再根据二次函数图象上点的坐标特征判断y1，y2，y3从小到大顺序．
解：∵二次函数y＝ax2+bx+c的图象过点A（1，2），B（3，2），C（5，7），
∴代入得：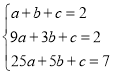
，
解得：a＝
，b＝
，c＝
，
对称轴是直线x＝
＝2，
∵a＝＞0，抛物线的开口向上，
在直线x＝2的左侧，y随x的增大而减小，
点K关于直线x＝2的对称轴是（﹣4，y3），
∵﹣4＜﹣2＜﹣1，
∴y3＞y1＞y2，
即y2＜y1＜y3，
故答案为：y2＜y1＜y3．
练习册系列答案
相关题目
