Question

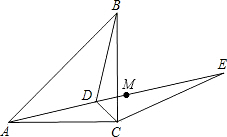
如图，在梯形ABCD中，已知AD∥BC，AB=CD，延长线段CB到E，使BE=AD，连接AE、AC．
（1）求证：△ABE≌△CDA；
（2）若∠DAC=40°，求∠EAC的度数

Answer 1

(1)证明见解析；（2）100°．

试题分析：（1）先根据题意得出∠ABE=∠CDA，然后结合题意条件利用SAS可判断三角形的全等；
（2）根据题意可分别求出∠AEC及∠ACE的度数，在△AEC中利用三角形的内角和定理即可得出答案．
（1）证明：在梯形ABCD中，∵AD∥BC，AB=CD，
∴∠ABE=∠BAD，∠BAD=∠CDA，
∴∠ABE=∠CDA
在△ABE和△CDA中，
，
∴△ABE≌△CDA．
（2）解：由（1）得：∠AEB=∠CAD，AE=AC，
∴∠AEB=∠ACE，
∵∠DAC=40°，
∴∠AEB=∠ACE=40°，
∴∠EAC=180°-40°-40°=100°．