题目内容
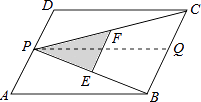
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2 , 若S=2,则S1+S2= . 
【答案】8
【解析】解:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,EF= ![]() BC,
BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S△PBC=1:4,S△PEF=2,
∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=8.
所以答案是:8
【考点精析】利用三角形中位线定理和平行四边形的判定与性质对题目进行判断即可得到答案,需要熟知连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.

练习册系列答案
相关题目