题目内容
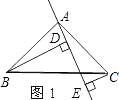
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB于点R,PS⊥AC于点S,若PR=PS,则下列结论正确的个数是( )
(1)PQ=PB; (2)AS=AR;(3)△BRP≌△PSC (4)∠C=∠SPC
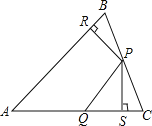
A. 1个 B. 2个 C. 3个 D. 4个
【答案】A
【解析】
根据到角的两边的距离相等的点在角的平分线上可得AP平分∠BAC,由直角三角形全等的判定方法得出Rt△ARP≌Rt△ASP,从而判断出(2)正确;根据由一组边相等和一组角相等无法判断△BRP≌△PSC,从而判断出(3)错误;同(3)也无法判断△BRP≌△PSQ,所以PQ≠PB,从而判断出(1)错误;△PSC是直角三角形,不一定是等腰直角三角形,所以∠C与∠SPC不一定相等,从而判断出(4)错误.
连接AP,
∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠A的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,![]() ,
,
∴Rt△ARP≌Rt△ASP,(HL),
∴AR=AS,∴(2)正确;
∵PR=PS,∠PRB=∠PSC=90°,
∴无法判断△BRP≌△PSC,故(3)错误;
∵∠PRB=∠PSQ=90°,PR=PS,
无法判断△BRP≌△PSQ,
∴PQ≠PB,故(1)错误;
∵△PSC是直角三角形,不一定是等腰直角三角形,
∴∠C与∠SPC不一定相等,故(4)错误;
故选:A.

练习册系列答案
相关题目