Question

【题目】如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在E处，EQ与BC相交于F．若AD=8cm，AB=6cm，AE=4cm．则△EBF的周长是cm．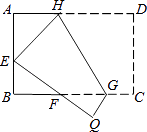

Answer 1

【答案】8
【解析】解：设AH=a，则DH=AD﹣AH=8﹣a，

在Rt△AEH中，∠EAH=90°，AE=4，AH=a，EH=DH=8﹣a，

∴EH2=AE2+AH2，即（8﹣a）2=42+a2，

解得：a=3．

∵∠BFE+∠BEF=90°，∠BEF+∠AEH=90°，

∴∠BFE=∠AEH．

又∵∠EAH=∠FBE=90°，

∴△EBF∽△HAE，

∴ = = = ．

∵C△HAE=AE+EH+AH=AE+AD=12，

∴C△EBF= C△HAE=8．

所以答案是：8．

【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对矩形的性质的理解，了解矩形的四个角都是直角，矩形的对角线相等．