题目内容
【题目】△ABD中,AB=BD,点C在直线BD上,BD=3CD,cos∠CAD= ![]() ,AD=6,则AC= .
,AD=6,则AC= .
【答案】6或 ![]()
【解析】解:分两种情况:①如图所示,当点C在线段BD上时,过B作BF⊥AD于F,过D作DE⊥AD交AC的延长线于E,

Rt△ADE中,cos∠CAD= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AE= ![]() , 分两种情况:①如图所示,当点C在线段BD上时,过B作BF⊥AD于F,过D作DE⊥AD交AC的延长线于E,在Rt△ADE中根据锐角三角函数的定义得出AE的长,
, 分两种情况:①如图所示,当点C在线段BD上时,过B作BF⊥AD于F,过D作DE⊥AD交AC的延长线于E,在Rt△ADE中根据锐角三角函数的定义得出AE的长,
∵BD=3CD,DE∥BF,
∴ ![]() =
= ![]() =
= ![]() ,
,
设CE=x,则CG=2x,GE=3x,
∵AB=BD,BF⊥AD,
∴AF=FD,
∴AG=GE=3x,
∴AE=6x,AC=5x,
∴AC= ![]() AE=
AE= ![]() ×
× ![]() =6;②如图所示,当C在BD的延长线上时,过B作BF⊥AD于F,过C作CE⊥AD交AD的延长线于E,
=6;②如图所示,当C在BD的延长线上时,过B作BF⊥AD于F,过C作CE⊥AD交AD的延长线于E,
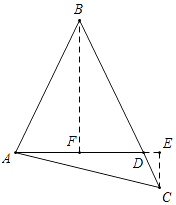
∵AB=BD,BF⊥AD,
∴AF=FD= ![]() AD=3,
AD=3,
∵CE∥BF,BD=3CD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即DE=1,
,即DE=1,
∴AE=6+1=7,
∵Rt△ACE中,cos∠CAD= ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AC= ![]() .
.
综上所述,AC的长为6或 ![]() .
.
所以答案是:6或 ![]() .
.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对平行线分线段成比例的理解,了解三条平行线截两条直线,所得的对应线段成比例.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】某体育用品商场为推销某一品牌运动服,先做了市场调查,得到数据如下表:
卖出价格x(元/件) | 50 | 51 | 52 | 53 |
销售量P(件) | 500 | 490 | 480 | 470 |
则P与x的函数关系式为________,当卖出价格为60元时,销售量为_______件.