题目内容
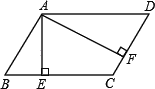
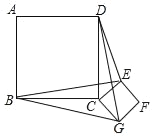
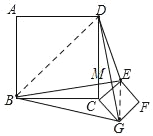
【题目】如图,正方形ABCD和正方形CEFG的边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论是( )
A. ①B. ②C. ①②D. ①②③
【答案】D
【解析】
根据正方形的性质易证△DCG≌△BEC,即可证得BE=DG,BE⊥DG,由此判断①②正确;根据勾股定理可得BD2=DM2+BM2,EG2=ME2+MG2,则BD2+EG2=DM2+BM2+ME2+MG2,可得BD2+EG2=BG2+DE2.再把a,b代入即可证得③正确.
如图:连接BD,EG,BE,DG的交点为M
∵四边形ABCD,四边形CEFG 为正方形
∴BC=DC,CG=CE,∠BCD=∠ECG,
∴∠BCE=∠DCG,且BC=DC,CG=CE,
∴△BCE≌△DCG,
∴DG=BE,∠CBE=∠CDE,
∵∠DBE+∠EBC+∠BDC+∠BCD=180°,
∴∠DBE+∠EBC+∠BDC=90°,
∵∠DBE+∠CDE+∠BDC+∠BMD=180°,
∴∠DCB=∠DMB=90°,
∴BE⊥DG故①②正确.
∵BE⊥DG,
∴BD2=DM2+BM2,EG2=ME2+MG2,
∴BD2+EG2=DM2+BM2+ME2+MG2,
∴BD2+EG2=BG2+DE2.
∴AB2+AD2+EC2+CG2=BG2+DE2.
∴2a2+2b2=BG2+DE2,故③正确
故选D.

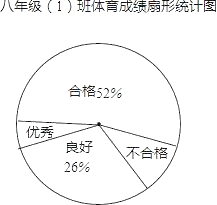
【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .