题目内容
【题目】如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°.求BC的长和四边形ABCD的面积.
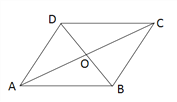
【答案】BC的长为12,四边形ABCD的面积为120
【解析】试题分析:根据勾股定理求得OA的长,再根据对角线互相平分的四边形是平行四边形证明四边形ABCD是平行四边形,从而根据平行四边形的对边相等就可求得BC的长;根据平行四边形的面积公式可以求得它的面积.
试题解析:在△AOD中,∠ADB=90°,AD=12,0D=5,
根据勾股定理,得
OA2=OD2+AD2=52+122=169,
∴OA=13.
∵AC=26,OA=13,
∴OA=OC,
又DO=OB,
∴四边形ABCD为平行四边形,
∴AD=BC=12;
∵∠ADB=90°,
∴AD⊥BD,
∴S四边形ABCD=ADBD=12×10=120,
答:BC的长为12,四边形ABCD的面积为120.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目