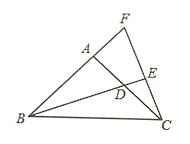
��Ŀ����
����Ŀ���ھ���ABCD�У���P��AD�ϣ�AB=3��AP=1�������ǰ��ֱ�Ƕ�����ڵ�P�������ǰ����ֱ�DZ߷ֱ�����AB��BC���ཻ�ڵ�E��F������EF��
��1����ͼ������E���B�غ�ʱ����Fǡ�����C�غϣ����ʱPC�ij���
��2�������ǰ�ӣ�1���е�λ�ÿ�ʼ���Ƶ�P˳ʱ����ת������E���A�غ�ʱֹͣ������������У�����۲졢̽�����������������У���CF=m���Խ�𣺢��ú�m�Ĵ���ʽ��ʾ�ı���BEPF���������ֱ��д��m��ȡֵ��Χ���ڴӿ�ʼ��ֹͣ�����߶�EF���е���������·�߳���
���𰸡���1��![]() ����2����S�ı���BEPF=15��
����2����S�ı���BEPF=15��![]() m����0��m��9������
m����0��m��9������![]() ��
��
��������
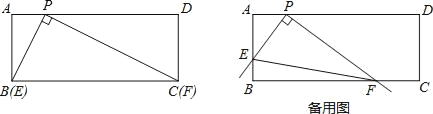
��1���������ABP�ס�DPC��ͨ�����������ʱPC�ij�
��2������F��FG��AD�ڵ�G����APE�ס�GFP����![]() ����Rt��EPF�У�tan��PEF=
����Rt��EPF�У�tan��PEF=![]() ��tan��PEF��ֵ���䣮
��tan��PEF��ֵ���䣮
���PEF�Ĵ�С���䣮

����Ŀ����ͼ������ABC�У���ACB��90����D��BC���е㣬DE��BC��CE//AD����AC��2��CE��4�����ı���ACEB���ܳ�Ϊ �� ��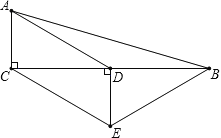
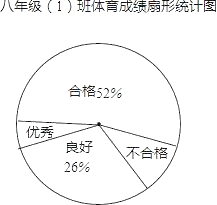
����Ŀ��ijУ�Ծ��꼶��1����ȫ��ѧ�������������ԣ����Գɼ���Ϊ���㡢���á��ϸ�Ͳ��ϸ��ĸ��ȼ������ݲ��Գɼ����ƵIJ�����ͳ��ͼ�����£�
���꼶��1���������ɼ�Ƶ���ֲ�����
�ȼ� | ��ֵ | Ƶ�� |
���� | ��90��100�� | |
���� | ��75��89�� | ��13 |
�ϸ� | ��60��74�� | |
���ϸ� | ��0��59�� | ��9 |
����ͳ��ͼ����������Ϣ������������⣺
��1�����꼶��1����ж�����ѧ����
��2�������ɼ�Ϊ�����Ƶ������ �����ϸ��Ƶ��Ϊ�� ����
��3�����Ըð������ɼ��ﵽ����̶ȵ�3��������2��Ů���������ȡ2�˲μ�ѧУ����������ǡ�ó鵽1��������1��Ů���ĸ������� ����