题目内容
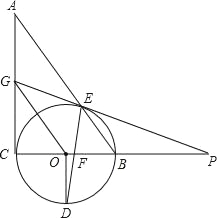
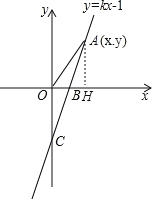
【题目】如图,直线y=kx-1与x轴、y轴分别交于B、C两点,OB:OC=![]() .
.
(1)求B点的坐标和k的值.
(2)若点A(x,y)是第一象限内的直线y=kx-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)在(2)的条件下,当点A运动到什么位置时,△AOB的面积是![]() .
.

【答案】(1)B(![]() ,0),OB=
,0),OB=![]() (2)S=
(2)S= ![]()
![]() ,(x>
,(x>![]() ) (3)A(
) (3)A(![]() ,
,![]() )
)
【解析】
(1)可先求出OC长,并用k的代数式表示点B的坐标及OB的长,然后在△BOC中运用三角函数可求出∠OCB的度数,再运用三角函数就可解决问题.
(2)过点A作AH⊥x轴于H,由于点A在直线y=kx-1上,因此可用x的代数式表示y,进而可得到S与x的函数关系式.
(3)把S=![]() 代入(2)中的解析式就可得到点A的横坐标,进而可得到点A的纵坐标.
代入(2)中的解析式就可得到点A的横坐标,进而可得到点A的纵坐标.
(1)在Rt△BOC中,
∵![]() =0,
=0,
∴k![]() 1=0.
1=0.
∴![]() =
=![]() .
.
∴点B的坐标为(![]() ,0),OB=
,0),OB=![]() .
.
∵![]() =0,∴
=0,∴![]() =01=1.
=01=1.
∴![]() =1.∴OC=1.
=1.∴OC=1.
∵sin∠OCB=![]() ,
,
∴∠OCB=30°.
∴tan∠OCB=![]() .
.
∴OB=![]() OC.
OC.
∴![]() =
=![]() ×1.
×1.
∴k=![]() .
.
∴B点坐标为(![]() ,0),k的值为
,0),k的值为![]() .
.
(2)过点A作AH⊥x轴于H,如图.
则有AH=y=![]() x1.x>
x1.x>![]() .
.
∴S=![]() OBAH=
OBAH=![]() ×
×![]() ×(
×(![]() x1)=
x1)= ![]()
![]() ,(x>
,(x>![]() ).
).
(3)当S△AOB=![]() 时,
时, ![]()
![]() =
=![]() .
.
解得;x=![]() .
.
∴y=![]() x 1=
x 1=![]() ×
×![]() 1=
1=![]() .
.
∴点A的坐标为(![]() ,
,![]() ).
).
∴当点A运动到点(![]() ,
,![]() )的位置时,△AOB的面积是
)的位置时,△AOB的面积是![]() .
.

【题目】某地台风带来严重灾害,该市组织20辆汽车装食品、药品、生活用品三种救灾物质共100吨到灾民安置点.按计划20辆汽车都要装运,每辆汽车只能装运同种物质且必须装满.根据表格提供的信息,解答下列问题:
物资种类 | 食品 | 药品 | 生活用品 |
每辆汽车运载量(吨) | 6 | 5 | 4 |
每吨所需运费(元/吨) | 120 | 160 | 100 |
(1)若装食品的车辆是5辆,装药品的车辆为__________辆;
(2)设装食品的车辆为x辆,装药品的车辆为y辆,求y与x的函数关系式;
(3)如果装食品的车辆不少于7辆,装药品的车辆不少于4辆,那么车辆的安排有几种方案?请写出每种方案并求出最少费用.