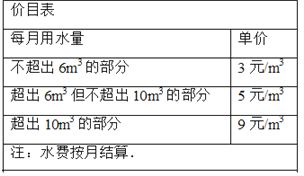
题目内容
【题目】仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:
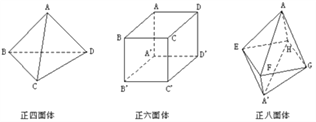
⑴填空:
①正四面体的顶点数V= ,面数F= ,棱数E= .
②正六面体的顶点数V= ,面数F= ,棱数E= .
③正八面体的顶点数V= ,面数F= ,棱数E= .
⑵若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用一个公式来表示,这就是著名的欧拉公式,请写出欧拉公式:
⑶如果一个多面体的棱数为30,顶点数为20,那么它有多少个面?
【答案】⑴①4,4,6;②8,6,12;③6,8,12;⑵V+F-E=2;⑶它有12个面.
【解析】试题分析:(1)观察图形,结合多面体的顶点,面,棱的定义进行填空即可,(2)根据(1)中,多面体的顶点数,面数,棱数,总结规律可得V,F,E之间的数量关系,(3)根据(2)中,顶点数,面数,和棱数之间的关系式代入求解即可.
解:⑴①4,4,6;②8,6,12;③6,8,12;
⑵V+F-E=2
⑶解:设面数为F,则20+F-30=2 解得F=12
答:它有12个面.

练习册系列答案
相关题目