题目内容
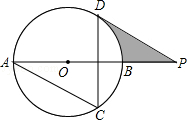
如图,AB是⊙O的直径,BC是⊙O的切线,连接AC交⊙O于点D,E为 上一点,连结AE,BE,BE交AC于点F,且AE2=EF•EB.
上一点,连结AE,BE,BE交AC于点F,且AE2=EF•EB.

(1)求证:CB=CF;
(2)若点E到弦AD的距离为1, ,求⊙O的半径.
,求⊙O的半径.
 上一点,连结AE,BE,BE交AC于点F,且AE2=EF•EB.
上一点,连结AE,BE,BE交AC于点F,且AE2=EF•EB.
(1)求证:CB=CF;
(2)若点E到弦AD的距离为1,
 ,求⊙O的半径.
,求⊙O的半径.(1)证明:如图,

∵AE2=EF•EB,∴ 。
。
又∠AEF=∠AEB,∴△AEF∽△AEB。
∴∠1=∠EAB。
∵BC是⊙O的切线,∴∠3=∠EAB。
又∵∠1=∠2,
∴∠2=∠3。∴CB=CF。
(2)如图,连接OE交AC于点G,设⊙O的半径是r,
由(1)知,△AEF∽△AEB,则∠EAF=∠EBA,∴ 。∴OE⊥AD。
。∴OE⊥AD。
∵点E到弦AD的距离为1,∴EG=1。
∵ ,且∠C+∠GAO=90°,∴
,且∠C+∠GAO=90°,∴ 。
。
∴ ,即
,即 。
。
解得, ,即⊙O的半径是
,即⊙O的半径是 。
。

∵AE2=EF•EB,∴
 。
。又∠AEF=∠AEB,∴△AEF∽△AEB。
∴∠1=∠EAB。
∵BC是⊙O的切线,∴∠3=∠EAB。
又∵∠1=∠2,
∴∠2=∠3。∴CB=CF。
(2)如图,连接OE交AC于点G,设⊙O的半径是r,
由(1)知,△AEF∽△AEB,则∠EAF=∠EBA,∴
 。∴OE⊥AD。
。∴OE⊥AD。∵点E到弦AD的距离为1,∴EG=1。
∵
 ,且∠C+∠GAO=90°,∴
,且∠C+∠GAO=90°,∴ 。
。∴
 ,即
,即 。
。解得,
 ,即⊙O的半径是
,即⊙O的半径是 。
。(1)如图,通过相似三角形(△AEF∽△AEB)的对应角相等推知,∠1=∠EAB;又由弦切角定理、对顶角相等证得∠2=∠3;最后根据等角对等边证得结论。
(2)如图,连接OE交AC于点G,设⊙O的半径是r,由(1)中的相似三角形的性质证得∠EAF=∠EBA,所以由“圆周角、弧、弦间的关系”推知点E是弧AD的中点,则OE⊥AD;然后通过解直角△ABC求得cos∠C
=sin∠GAO= ,即可求得r的值。
,即可求得r的值。
(2)如图,连接OE交AC于点G,设⊙O的半径是r,由(1)中的相似三角形的性质证得∠EAF=∠EBA,所以由“圆周角、弧、弦间的关系”推知点E是弧AD的中点,则OE⊥AD;然后通过解直角△ABC求得cos∠C
=sin∠GAO=
 ,即可求得r的值。
,即可求得r的值。 
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
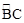 的弧长为 .
的弧长为 .