��Ŀ����
ij�Ϲ������г���Ϊָ��ij��ij���߲˵����������ۣ��ڶ������г������������������˵���Ļ����ϣ��Խ��������߲����к���г��ۼۺ������ɱ�������Ԥ�⣬�ṩ�������������Ϣ����ͼ�ס�����ͼ��
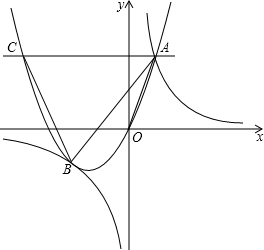
ע����ͼ�е�ÿ��ʵ�ĺڵ�����Ӧ��������ֱ�ָ��Ӧ�·ݵ��ۼۺͳɱ��������ɱ�6�·���ͣ�ͼ��ͼ�����߶Σ�ͼ�ҵ�ͼ���������ߣ�
��1����3�·ݳ��������߲ˣ�ÿǧ�˵����棨����=�ۼ�-�ɱ����Ƕ���Ԫ
��2����x�·ݳ��������߲ˣ�ÿǧ������ΪyԪ����y����x�ĺ�������ʽ��
��3�����ĸ��³��������߲ˣ�ÿǧ�˵��������˵�����ɣ�

ע����ͼ�е�ÿ��ʵ�ĺڵ�����Ӧ��������ֱ�ָ��Ӧ�·ݵ��ۼۺͳɱ��������ɱ�6�·���ͣ�ͼ��ͼ�����߶Σ�ͼ�ҵ�ͼ���������ߣ�
��1����3�·ݳ��������߲ˣ�ÿǧ�˵����棨����=�ۼ�-�ɱ����Ƕ���Ԫ
��2����x�·ݳ��������߲ˣ�ÿǧ������ΪyԪ����y����x�ĺ�������ʽ��
��3�����ĸ��³��������߲ˣ�ÿǧ�˵��������˵�����ɣ�

��1����3�·ݣ�ÿǧ���ۼ�Ϊ5Ԫ����3�·ݣ�ÿǧ�˳ɱ�Ϊ4Ԫ
����3�·ݳ��������߲ˣ�ÿǧ��������5-4=1��Ԫ������2�֣�
��2����x�·ݳ���ʱ��ÿǧ���ۼ�Ϊy1Ԫ��ÿǧ�˳ɱ�Ϊy2Ԫ
����ͼ����y1=kx+b
��
��
��
��y1=-
x+7��5�֣�
����ͼ����y2=a��x-6��2+1
��4=a��3-6��2+1
��a=
��y2=
(x-6)2+1
��y=y1-y2
��y=-
x+7-[
(x-6)2+1]
��y=-
x2+
x-6
��3����y=-
x2+
x-6
��y=-
(x-5)2+
��
�൱x=5ʱ��y�����ֵ������5�·ݳ���ʱ��ÿǧ���������
����3�·ݳ��������߲ˣ�ÿǧ��������5-4=1��Ԫ������2�֣�
��2����x�·ݳ���ʱ��ÿǧ���ۼ�Ϊy1Ԫ��ÿǧ�˳ɱ�Ϊy2Ԫ
����ͼ����y1=kx+b
��
|
��
|
��y1=-
| 2 |
| 3 |
����ͼ����y2=a��x-6��2+1
��4=a��3-6��2+1
��a=
| 1 |
| 3 |
��y2=
| 1 |
| 3 |
��y=y1-y2
��y=-
| 2 |
| 3 |
| 1 |
| 3 |
��y=-
| 1 |
| 3 |
| 10 |
| 3 |
��3����y=-
| 1 |
| 3 |
| 10 |
| 3 |
��y=-
| 1 |
| 3 |
| 7 |
| 3 |
�൱x=5ʱ��y�����ֵ������5�·ݳ���ʱ��ÿǧ���������

��ϰ��ϵ�д�
�����Ŀ
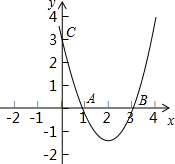
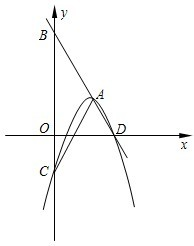
 �㣬��y�ύ��C�㣬��A��C����Ϊ��2��0������0��3����
�㣬��y�ύ��C�㣬��A��C����Ϊ��2��0������0��3����
 x2���ң�x1+1����x2+1��=5
x2���ң�x1+1����x2+1��=5