Question

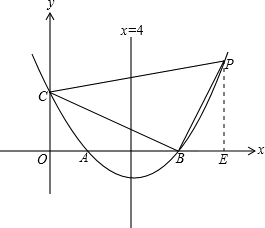
如图所示，已知抛物线的对称轴为直线x=4，该抛物线与x轴交于A、B两点，与y轴交于C点，且A、C坐标为（2，0）、（0，3）．
（1）求此抛物线的解析式；
（2）抛物线上有一点P，使以PC为直径的圆过B点，求P的坐标；
（3）在满足（2）的条件下，x轴上是否存在点E，使得△COE与△PBC相似？若存在，求出E的坐标；若不存在，请说明理由．

Answer 1

（1）设抛物线的解析式是y=a（x-4）²+b，
根据题意得：

4a+b=0 16a+b=3

，
解得：

a= 1 4 b=-1

，
则函数的解析式是：y=

1

4

x²-2x+3；

（2）设点B坐标为B（a，0），则

2+a

2

=4（抛物线对称轴的表示），
解得a=6，
∴点B（6，0），
又∵点C坐标为C（0，3），PC为直径的圆过B点，
∴过P作PE⊥x轴，则△PBE∽△BCO，

∴

PE

BE

=

OB

OC

=

6

3

=2，
∴设点P的坐标为（m，n），
则n=2（m-6）①，
又点P在抛物线上，
∴n=

1

4

m²-2m+3②，
①②联立解得m₁=10，m₂=6（舍去），
∴n=2（10-6）=8，
∴点P的坐标为P（10，8）；

（3）∵PE⊥x轴，
∴在Rt△PBE中，PB

(10-6)2+82

=4

5

，
在Rt△OBC中，BC=

32+62

=3

5

，
设点E坐标为（x，0），
∵△COE与△PBC相似，
∴①若CO与PB是对应边，则

3

4 5

=

|x|

3 5

，
解得|x|=

9

4

，
∴x=±

9

4

，
②若CO与BC是对应边，则

3

3 5

=

|x|

4 5

，
解得|x|=4，
∴x=±4，
∴在x轴上存在点E，使得△COE与△PBC相似，点E坐标为E（±

9

4

，0），E（±4，0）．