Question

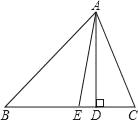
【题目】如图，某武警部队在一次地震抢险救灾行动中，探险队员在相距4米的水平地面A，B两处均探测出建筑物下方C处有生命迹象，已知在A处测得探测线与地面的夹角为30°，在B处测得探测线与地面的夹角为60°，求该生命迹象C处与地面的距离．（结果精确到0.1米，参考数据： ≈1.41， ≈1.73）

Answer 1

【答案】解：过C点作AB的垂线交AB的延长线于点D，

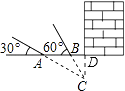
∵∠CAD=30°，∠CBD=60°，

∴∠ACB=30°，

∴∠CAB=∠ACB=30°，

∴BC=AB=4米，

在Rt△CDB中，BC=4米，∠CBD=60°，sin∠CBD= ，

∴sin60°= ，

∴CD=4sin60°=4× =2 ≈3.5（米），

故该生命迹象所在位置的深度约为3.5米．

【解析】本题考查的是解直角三角形的应用，先根据题意先过C点作AB的垂线交AB的延长线于点D，由三角形外角的性质可得出∠ACB=30°，进而可得出BC=AB=4米，在Rt△CDB中利用锐角三角函数的定义即可求出CD的值．
【考点精析】根据题目的已知条件，利用关于坡度坡角问题的相关知识可以得到问题的答案，需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA．