题目内容
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲骑自行车从
两地,甲骑自行车从![]() 地到
地到![]() 地;乙骑自行车从
地;乙骑自行车从![]() 地到
地到![]() 地,到达
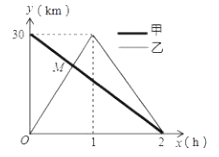
地,到达![]() 地后立即按原路返回,如图是甲乙两人离
地后立即按原路返回,如图是甲乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图像,根据图像解答以下问题:
之间的函数图像,根据图像解答以下问题:
(1)求出甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(2)求出点![]() 的坐标,并解释改点坐标所表示的实际意义;
的坐标,并解释改点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过![]() 时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时
时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2) 点M的坐标是(
;(2) 点M的坐标是(![]() ,20),点M的坐标表示:甲、乙经过
,20),点M的坐标表示:甲、乙经过![]() h第一次相遇,此时离点B的距离是20km;(3)
h第一次相遇,此时离点B的距离是20km;(3) ![]() 当或
当或![]() ≤x≤2.
≤x≤2.
【解析】
(1) 根据函数图象就可以得出A, C点坐标,用待定系数法可得甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(2) 根据函数图象求出OC的解析式,求出OC与AB的交点可得M点坐标, 根据图像可得M的坐标表示的含义;
(3) 分情况讨论,当![]() -
-![]() ≤3,
≤3,![]() -
-![]() ≤3,分别求出x的值可以得出结论.
≤3,分别求出x的值可以得出结论.
解:如图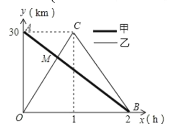
可得甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式即为AC的函数表达式,
之间的函数表达式即为AC的函数表达式,
其经过点A(0,30),B(2,0),
设其表达式为:![]() ,可得
,可得![]() ,
,
解得:![]() ,
,
甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式为:
之间的函数表达式为:![]() .
.
(2) 设OC的解析式为![]() ,其经过点C(1,30),
,其经过点C(1,30),
可得![]() =30,
=30,![]()
![]() ;
;
设BC的解析式为![]() ,其经过点C(1,30),B(2,0),
,其经过点C(1,30),B(2,0),
可得:![]() ,解得
,解得![]() ,
,
![]()
![]()
![]()
![]()
可得M点为AB与OC的交点,![]() =
=![]() 可得-15x+30=30x,
可得-15x+30=30x,
解得:x=![]() ,
,![]()
![]() =
=![]() =20,
=20,
![]() 点M的坐标是(
点M的坐标是(![]() ,20),点M的坐标表示:甲、乙经过
,20),点M的坐标表示:甲、乙经过![]() h第一次相遇,此时离点B的距离是20km;
h第一次相遇,此时离点B的距离是20km;
(3)分情况讨论:
①![]() -
-![]() ≤3,
≤3,![]() -
-![]() ≤3时
≤3时
![]() 解得:
解得:![]()
②(-30x+60)-(15x+30)≤3
解得:x≥![]()
![]()
![]() ≤x≤2
≤x≤2
综上所述:![]() 当或
当或![]() ≤x≤2两人能够用无线对讲机保持联系.
≤x≤2两人能够用无线对讲机保持联系.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目