题目内容
【题目】如图,Rt△ABC中,∠BAC=90°,E是AC的中点,AE=2.经过点E作△ABE外接圆的切线交BC于点D,过点C作CF⊥BC交BE的延长线于点F,连接FD交AC于点H,FD平分∠BFC.
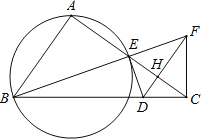
(1)求证:DE=DC;
(2)求证:HE=HC=1;
(3)求BD的长度.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据切线的定义证得DE⊥BF;然后由角平分线的性质(角平分线上的点到这个角的两边距离相等)证得DE=DC;
(2)根据全等直角三角形的判定定理HL证得Rt△DEF≌Rt△DCF;然后由全等三角形的对应角相等、等腰三角形的“三合一”的性质推知CH=CE=1;
(3)由相似三角形△ABC∽△AEB的对应边成比例求得AB=2![]() ;然后在Rt△ABE中利用正切三角函数的定义推知tan∠ABE=
;然后在Rt△ABE中利用正切三角函数的定义推知tan∠ABE=![]() ;最后由勾股定理、等角的三角函数值相等即可求得BC、CD的长度,从而求得BD=BC-CD.
;最后由勾股定理、等角的三角函数值相等即可求得BC、CD的长度,从而求得BD=BC-CD.
(1)证明:∵∠BAC=90°,
∴BE是△ABE外接圆的直径;
又∵DE是△ABE外接圆的切线,
∴DE⊥BF;
又∵CF⊥BC,FD平分∠BFC,
∴DE=DC;
(2)证明:∵E是AC的中点,AE=2,
∴CE=AE=2;
在Rt△DEF和Rt△DCF中,
![]() ,
,
∴Rt△DEF≌Rt△DCF(HL),
∴∠EDH=∠CDH,
∴DH是CE边上的中线,DH⊥CE,
∴HE=HC=1;
(3)∵∠ABE+∠AEB=90°,∠AEB=∠FEH,∠FEH+∠DEH=90°,
∴∠ABE=∠DEH=∠DCH,
又∵∠A=∠A,
∴△ABC∽△AEB,
∴AB:AC=AE:AB,
∵AE=2,AC=2AE=4,
∴AB=2![]() ,
,
∴tan∠ABE=![]() ;
;
∴在Rt△ABC中,根据勾股定理知,BC=2![]() ;
;
∵tan∠ABE=tan∠DCH=![]() ,
,
∴DH=![]() ,
,
∴CD=![]() ,
,
∴BD=BC-CD=![]() .
.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案