Question

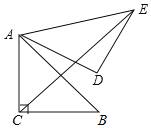
【题目】如图，在△ABC中，AC=BC，∠ACB=90°，AB=4，将△ABC绕点A逆时针旋转60°，得到△ADE，连接CE，则CE等于（　　）

A. 5B. 6C. 2+2D. 2+2

Answer 1

【答案】C

【解析】

首先考虑到CE所在的三角形并不是特殊三角形，所以猜想到要求CE，可能需要构造直角三角形．由旋转的性质可知，AB=AE，∠BAE=60°，故△ABE是等边三角形，可证明△ACE与△CBE全等，可得到∠ACE=45°，∠AEC=30°，再证△AFC和△AFE是直角三角形，然后在根据勾股定理求解．

连结BE，设CE与AB相交于点F，如下图所示，

∵Rt△ABC中，AC=BC，∠ACB=90°

∴∠CBA=∠BAC=45°

∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合，

∴∠BAC=∠DAE=45°，AB=AE

又∵旋转角为60°

∴∠CAD=∠BAE=60°，

∴△ABE是等边三角形

∴AB=BE=AE=4

在△ACE与△CBE中，

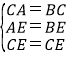
∴△ACE≌△CBE （SSS）

∴∠ACE=∠CBE=45°，∠CEB=∠AEC=30°

∴在△ACF中，∠CFA=180°-45°-45°=90°

∴∠AFC=∠AFE=90°

∴CF⊥AB，∵CA=CB，∠ACB=90°，

∴CF=AF=FB=2，

又在Rt△AFE中，∠AEF=30°，

∴FE=AF=2，

∴CE=CF+FE=2+2.

故选C．