题目内容
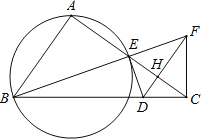
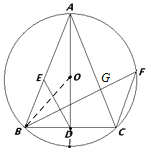
【题目】已知：如图，
内接于
，
，点
为弦
的中点，
的延长线交
于点
，联结
，过点
作
交于点
，联结
.
（1）求证：
；
（2）如果的半径为8，且
，
，求的长.
【答案】(1)证明见解析；（2）CF=12
-12.
【解析】
由等腰三角形的性质得出
，由垂径定理得出
，
，证出DE是
的中位线
得出
，结合BF⊥DE证出
，由角的互余关系即可得出结论；
连接
证出
是等腰直角三角形，得出
再由等腰三角形的性质得出
即可得出结论．
证明：如图1所示：
，
，
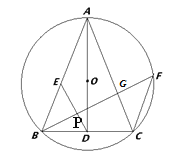
直线AD经过圆心O，
，，
点E为弦AB的中点，
是的中位线．
，
，
，
，
．
，
，
，
又
，
，
；
证明：连接如图所示：
，
，
是等腰直角三角形，
．
，
，且，
．
∴∠BFC=
=45°，
，
和△CFG均为等腰直角三角形，
AB．CG=FG=
FC；
∵AC=AB=BF=12
∴AG=BG=6
，CG=FG=12-6
∴CF=（12-6）×=12-12
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
