Question

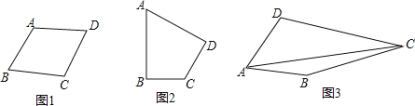
【题目】类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．

概念理解：

如图，在四边形中，添加一个条件使得四边形是“等邻边四边形”．请写出你添加的一个条件，你添加的条件是________．

问题探究：

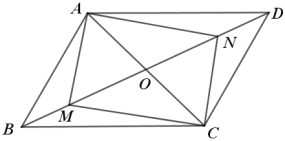
如图，在“等邻边四边形”中，，，，求对角线的长．

拓展应用：

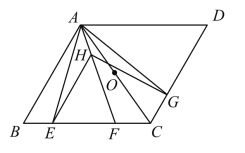
如图，“等邻边四边形”中，，，，为对角线，试探究，，的数量关系．

Answer 1

【答案】（1）．（2）；（3）

【解析】

（1）根据定义可知：只需要一组邻边相等即可．

（2）由AB=AD，∠BAD=60°，可知△ABD是等边三角形，再由∠ABC=∠ADC=90°，可知CB=CD，所以AC垂直平分BD，然后利用直角三角形的相关性质分别计算出AO和OC的长度．

（3）由于∠BAD+∠BCD=90°，所以考虑构造直角三角形使得该直角三角形的三边长度分别是AC、BC、CD的长度，然后利用勾股定理即可得出AC2=BC2+CD2

（1）根据定义：AB=BC．

（2）连接AC、BD交于点O，如图，

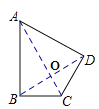
∵AB=AD，∠BAD=60°，

∴△ABD是等边三角形，

∴∠ABD=∠ADB=60°，

∵∠ABC=∠ADC=90°，

∴∠CBD=∠CDB=30°，

∴CB=CD，

∴AC垂直平分BD，

∴，

∴，

在Rt△BOC中，

，

∴OC=，

∴AC=AO+OC=4；

（3）过点C作CE⊥BC于点C，且使得CE=CD，

∵∠BAD+∠BCD=90°，

∴∠DCE=60°，

∴△CDE是等边三角形，

∴DE=CD，∠EDC=60°，

∵AB=AD，∠DAB=60°，

∴△ABD是等边三角形，

∴AD=BD，∠ADB=60°，

在△ADC和△BDE中，

，

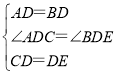∴△ADC≌△BDE（SAS），

∴AC=BE，

∵∠BCE=90°，

∴BE2=BC2+CE2，

即AC2=BC2+CD2