题目内容
【题目】(满分10分)已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
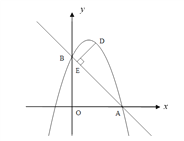
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,求直线AB与这个二次函数的解析式;
(3)在直线AB上方的抛物线上有一动点D,当D与直线AB的距离DE最大时,求点D的坐标,并求DE最大距离是多少?
【答案】(1) m>-1;(2) 直线AB的解析式为y=-x+3, 抛物线解析式为y=-x2+2x+3;(3) DE的最大值为![]() .
.
【解析】试题分析:(1)根据抛物线与x轴有两个交点时,△>0,即可得到结论;
(2)把点A(3,0)代入y=-x2+2x+m得到-9+6+m=0得到B(0,3),解方程组即可得到结论;
(3)过点D作y轴的垂线,垂足为C,再过点A作AG⊥CD,垂足为G,连接BD,AD,得到当DE的值越大时,S△ADB的面积越大,设D(x,y),DC=x,BC=y-3,DG=3-x,AG=y根据图形的面积公式即可得到结论.
试题解析:
(1)当抛物线与x轴有两个交点时,△>0,即4+4m>0,
∴m>-1.
(2) ∵点A(3,0)在抛物线y=-x2+2x+m上,
∴-9+6+m=0,∴m=3.
∴抛物线解析式为y=-x2+2x+3,且B(0,3).
设直线AB的解析式为y=kx+b,将A(3,0),B(0,3)代入y=kx+b中,得到
![]()
解得![]() ,∴直线AB的解析式为y=-x+3.
,∴直线AB的解析式为y=-x+3.
(3)过点D作y轴的垂线,垂足为C,再过点A作AG⊥CD,垂足为G,连接BD,AD.
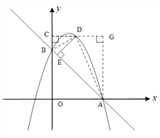
∵AB为定值,∴当DE的值越大时, ![]() 的面积越大.
的面积越大.
设D(x,y),DC=x,BC=y-3,DG=3-x,AG=y
∴![]()
![]()
![]()
∵![]() ∴当
∴当![]() 时,
时, ![]()
将![]() 代入y=-x2+2x+3,得到
代入y=-x2+2x+3,得到![]() ,即D(
,即D(![]() ,
, ![]() )
)
又∵![]() ,且
,且![]()
∴![]() .
.
∴![]()
答:DE的最大值为![]() .
.

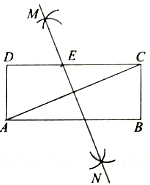
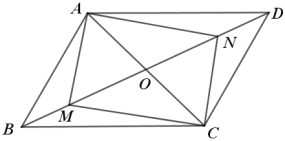
【题目】如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
【题目】我国淡水资源短缺问题十分突出,节约用水已成为各地的一件大事.某校初三学生为了调查居民用水情况,随机抽查了某小区10户家庭的月用水量,结果如表所示:
月用水量(t) | 3 | 4 | 5 | 10 |
户数 | 4 | 2 | 3 | 1 |
这10户家庭月用水量的平均数、中位数及众数是( )
A. 4.5,3,4B. 3,4.5,4C. 4.5,4,3D. 4,4.5,3