题目内容
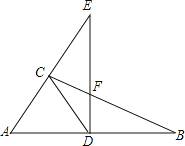
【题目】如图，
，OC平分
，C为角平分线上一点，过点C作
，垂足为C，交OB于点D，
交OB于点E．
判断
的形状，并说明理由；
若
，求CD的长．
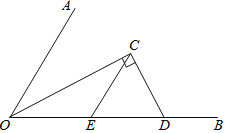
【答案】（1）等边三角形（2）
【解析】
（1）△CED为等边三角形，理由如下：由OC为角平分线及∠AOB度数求出∠AOC与∠COE度数，再由CE与OA平行，得到一对内错角相等，再由CD与OC垂直，求出∠ECD度数，利用三个内角相等的三角形为等边三角形即可得证；
（2）由△CED为等边三角形，得到三边相等，利用等角对等边得到OE=CE，进而得到OE=CE=DE，设CD=x，利用30度角所对的直角边等于斜边的一半得到OD=2x，再由OC的长，利用勾股定理列出方程，求出方程的解得到x的值，即可确定出CD的长．
是等边三角形，理由如下：
平分
，
，
，
，
，
，
，
，
，
是等边三角形；
是等边三角形，
，
又
，
，
，
设
，则
，
在
中，根据勾股定理得：
，
解得：
，
则
．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
