题目内容
【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.
(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
【答案】
(1)
解:如图所示,
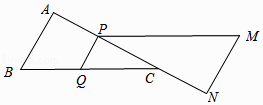
AB=3cm,BC=5cm,AC⊥AB,
∴Rt△ABC中,AC=4,
若PQ∥AB,则有 ![]() =
= ![]() ,
,
∵CQ=PA=t,CP=4﹣t,QB=5﹣t,
∴ ![]() =
= ![]() ,
,
即20﹣9t+t2=t2,
解得t= ![]() ,
,
当t= ![]() 时,PQ∥AB
时,PQ∥AB
(2)
解:如图所示,过点P作PD⊥BC于点D,
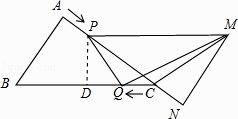
∴∠PDC=∠A=90°,
∵∠PCD=∠BCA
∴△CPD∽△CBA,
∴ ![]() =
= ![]() ,
,
当t=3时,CP=4﹣3=1,
∵BA=3,BC=5,
∴ ![]() =
= ![]() ,
,
∴PD= ![]() ,
,
又∵CQ=3,PM∥BC,
∴S△QMC= ![]() ×3×
×3× ![]() =
= ![]() ;
;
(3)
解:存在时刻t= ![]() ,使PQ⊥MQ,
,使PQ⊥MQ,
理由如下:如图所示,过点M作ME⊥BC的延长线于点E,
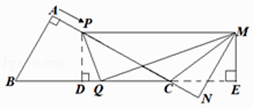
∵△CPD∽△CBA,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵BA=3,CP=4﹣t,BC=5,CA=4,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴PD= ![]() (4﹣t),CD=
(4﹣t),CD= ![]() (4﹣t).
(4﹣t).
∵PQ⊥MQ,
∴∠PDQ=∠QEM=90°,∠PQD=∠QME,
∴△PDQ∽△QEM,
∴ ![]() =
= ![]() ,即PDEM=QEDQ.
,即PDEM=QEDQ.
∵EM=PD= ![]() (4﹣t)=
(4﹣t)= ![]() ﹣
﹣ ![]() t,
t,
DQ=CD﹣CQ= ![]() (4﹣t)﹣t=
(4﹣t)﹣t= ![]() ﹣
﹣ ![]() t,
t,
QE=DE﹣DQ=5﹣[ ![]() (4﹣t)﹣t]=
(4﹣t)﹣t]= ![]() +
+ ![]() t,
t,
∴( ![]() ﹣
﹣ ![]() t)2=(
t)2=( ![]() ﹣
﹣ ![]() t)(
t)( ![]() +
+ ![]() t),
t),
即2t2﹣3t=0,
∴t= ![]() 或t=0(舍去),
或t=0(舍去),
∴当t= ![]() 时,PQ⊥MQ.
时,PQ⊥MQ.
【解析】(1)根据勾股定理求出AC,根据PQ∥AB,得出关于t的比例式,求解即可;(2)过点P作PD⊥BC于D,根据△CPD∽△CBA,列出关于t的比例式,表示出PD的长,再根据S△QMC= ![]() QCPD,进行计算即可;(3)过点M作ME⊥BC的延长线于点E,根据△CPD∽△CBA,得出PD=
QCPD,进行计算即可;(3)过点M作ME⊥BC的延长线于点E,根据△CPD∽△CBA,得出PD= ![]() (4﹣t),CD=
(4﹣t),CD= ![]() (4﹣t),再根据△PDQ∽△QEM,得到
(4﹣t),再根据△PDQ∽△QEM,得到 ![]() =
= ![]() ,即PDEM=QEDQ,进而得到方程(
,即PDEM=QEDQ,进而得到方程( ![]() ﹣
﹣ ![]() t)2=(
t)2=( ![]() ﹣
﹣ ![]() t)(
t)( ![]() +
+ ![]() t),求得t=
t),求得t= ![]() 或t=0(舍去),即可得出当t=
或t=0(舍去),即可得出当t= ![]() 时,PQ⊥MQ.
时,PQ⊥MQ.
【考点精析】关于本题考查的相似三角形的应用,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.

 阅读快车系列答案
阅读快车系列答案