题目内容
【题目】如图，已知动点P在函数y= 
（x＞0）的图象上运动，PM⊥x轴于点M，PN⊥y轴于点N，线段PM、PN分别与直线AB：y=﹣x+1交于点E，F，则AFBE的值为（ ）
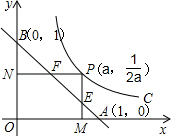
A.4
B.2
C.1
D.
【答案】C
【解析】解：作FG⊥x轴，
∵P的坐标为（a， 
），且PN⊥OB，PM⊥OA，
∴N的坐标为（0， ），M点的坐标为（a，0），
∴BN=1﹣ ，
在直角三角形BNF中，∠NBF=45°（OB=OA=1，三角形OAB是等腰直角三角形），
∴NF=BN=1﹣ ，
∴F点的坐标为（1﹣ ， ），
同理可得出E点的坐标为（a，1﹣a），
∴AF2=（1﹣1+ ）2+（ ）2= 
，BE2=（a）2+（﹣a）2=2a2 ，
∴AF2BE2= 2a2=1，即AFBE=1．
故选C．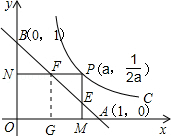
练习册系列答案
名校课堂系列答案
相关题目
