题目内容
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度为 ![]() (即tan∠PCD=
(即tan∠PCD= ![]() ).
).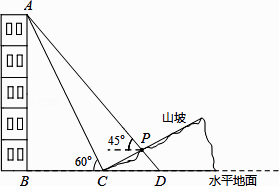
(1)求该建筑物的高度(即AB的长).
(2)求此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
【答案】
(1)
解:过点P作PE⊥BD于E,PF⊥AB于F,
又∵AB⊥BC于B,
∴四边形BEPF是矩形,
∴PE=BF,PF=BE
∵在Rt△ABC中,BC=90米,∠ACB=60°,
∴AB=BCtan60°=90 ![]() (米),
(米),
故建筑物的高度为90 ![]() 米;
米;
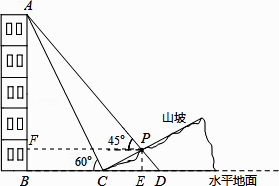
(2)
解:设PE=x米,则BF=PE=x米,
∵在Rt△PCE中,tan∠PCD= ![]() =
= ![]() ,
,
∴CE=2x,
∵在Rt△PAF中,∠APF=45°,
∴AF=AB﹣BF=90 ![]() ﹣x,
﹣x,
PF=BE=BC+CE=90+2x,
又∵AF=PF,
∴90 ![]() ﹣x=90+2x,
﹣x=90+2x,
解得:x=30 ![]() ﹣30,
﹣30,
答:人所在的位置点P的铅直高度为( ![]() )米
)米
【解析】(1)过点P作PE⊥BD于E,PF⊥AB于F,在Rt△ABC中,求出AB的长度即可;(2)设PE=x米,则BF=PE=x米,根据山坡坡度为 ![]() ,用x表示CE的长度,然后根据AF=PF列出等量关系式,求出x的值即可.
,用x表示CE的长度,然后根据AF=PF列出等量关系式,求出x的值即可.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.

练习册系列答案
相关题目