题目内容
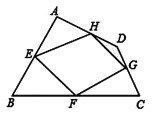
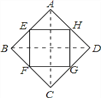
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是_____,证明你的结论;
(2)当四边形ABCD的对角线满足_____条件时,四边形EFGH是矩形(不证明)
(3)你学过的哪种特殊四边形的中点四边形是矩形?_____(不证明)
【答案】 平行四边形 互相垂直 菱形
【解析】分析:(1)、连接BD,根据三角形中位线的性质得出EH∥FG,EH=FG,从而得出平行四边形;(2)、首先根据三角形中位线的性质得出平行四边形,根据对角线垂直得出一个角为直角,从而得出矩形;(3)、根据菱形的性质和三角形中位线的性质得出平行四边形,然后根据对角线垂直得出矩形.
详解:(1)证明:连结BD.
∵E、H分别是AB、AD中点, ∴EH∥BD,EH=![]() BD,
BD,
同理FG∥BD,FG=![]() BD, ∴EH∥FG,EH=FG, ∴四边形EFGH是平行四边形
BD, ∴EH∥FG,EH=FG, ∴四边形EFGH是平行四边形
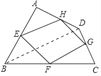
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.
理由如下:如图,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点, ∴EH∥BD,HG∥AC,
∵AC⊥BD, ∴EH⊥HG, 又∵四边形EFGH是平行四边形, ∴平行四边形EFGH是矩形;
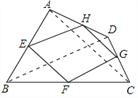
(3)菱形的中点四边形是矩形.理由如下:如图,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,∴EH∥BD,HG∥AC,FG∥BD,EH=![]() BD,FG=
BD,FG=![]() BD, ∴EH∥FG,EH=FG,
BD, ∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.∵四边形ABCD是菱形, ∴AC⊥BD,∵EH∥BD,HG∥AC,
∴EH⊥HG, ∴平行四边形EFGH是矩形.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案