Question

【题目】在⊙O中直径为4，弦AB＝2，点C是圆上不同于A、B的点，那么∠ACB度数为_____．

Answer 1

【答案】60°或120°．

【解析】

连接OA、OB，过O作AB的垂线，通过解直角三角形，易求得圆心角∠AOB的度数，然后根据C在优弧AB和劣弧AB上两种情况分类求解．

解：如图：过O作OD⊥AB于D，连接OA、OB．

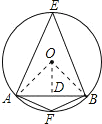
Rt△OAD中，OA=2，AD=，

∴∠AOD=60°，∠AOB=120°，

∴∠AEB=∠AOB=60°．

∵四边形AEBF内接于⊙O，

∴∠AFB=180°-∠AEB=120°．

①当点C在优弧AB上时，∠ACB=∠AEB=60°；

②当点C在劣弧AB上时，∠ACB=∠AFB=120°；
故∠ACB的度数为60°或120°．

故答案为：60°或120°．