题目内容
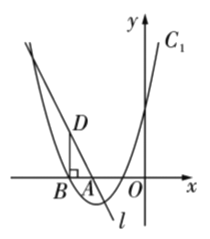
【题目】如图,在△ABC中,∠ACB=90°,AC=6,BC=8,动点E从点A出发沿着线段AB向终点B运动,速度为每秒3个单位长度,过点E作EF⊥AB交直线AC于点F,连结CE.设点E的运动时间为t秒.
(1)当点F在线段AC上(不含端点)时,
①求证:△ABC∽△AFE;
②当t为何值时,△CEF的面积为1.2;
(2)在运动过程中,是否存在某时刻t,使△CEF为等腰三角形?若存在,求出t的值;若不存在,请说明理由.

【答案】(1)①见解析;②![]() 秒或1秒;(2)存在,
秒或1秒;(2)存在,![]() 秒或
秒或![]() 秒
秒
【解析】
(1)①根据相似三角形的判定解答即可;
②过点 C 作 CH⊥AB 于 H,利用相似三角形的性质和三角形面积公式解答即可;
(2)根据等腰三角形的判定分两种情况解答.
解:(1)当点 F 在线段 AC 上时,
①证明如下:∵EF⊥AB,
∴∠AEF=90°
在△ABC 中,∠ACB=90°
∴∠ACB=∠AEF 又∵∠A=∠A
∴△ABC∽△AFE
②当 t 秒时,AE=3t, 由①得△ABC∽△AFE
∴![]() ,即
,即![]() ,
,
∴FE=4t
在 Rt△ABC 中,AB=![]()
![]() ,
,

过点 C 作 CH⊥AB 于 H,如图 1:
由面积法可得:![]()
∴![]()
∴![]()
=![]()
![]() .
.
令![]() ,
,
解得:![]() ,
,
经检验,符合题意.
答:当 t 为![]() 秒或 1 秒时,△CEF 的面积为 1.2.
秒或 1 秒时,△CEF 的面积为 1.2.
(2)存在,理由如下:
i)当点 F 在线段 AC 上时(0<t<![]() ),
),
∵∠CFE=∠AEF+∠A>90°,
∴当△CEF 为等腰三角形时,只能是 FC=FE,
由②可知:FE=4t,
∴AF=5t,FC=4t,
∴5t+4t=6,
∴t=![]() .
.
ii)当点 F 在线段 AC 的延长线上时(![]() <t
<t![]() ),如图 2,
),如图 2,
∵∠FCE=∠FCB+∠ECB>90°,
∴当△CEF 为等腰三角形时,只能是 FC=EC,
此时∠F=∠CEF,
∵EF⊥AB,
∴∠AEF=90°,即∠CEA+∠CEF=90°, 又∠F+∠A=90°
∴∠CEA=∠A,
∴CE=AC=6,
∴FC=6,
∴AF=12, 即 5t=12
∴![]()
综上所述,t 的值为![]() 秒或
秒或![]() 秒时,△CEF 为等腰三角形.
秒时,△CEF 为等腰三角形.


【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,具体过程如下:
收集数据
从八、九两个年级各随机抽取20名学生进行体质健康测试,测试成绩(百分制)如下:
八年级 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
九年级 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
整理、描述数据
将成绩按如下分段整理、描述这两组样本数据:
成绩(x) | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
八年级人数 | 0 | 0 | 1 | 11 | 7 | 1 |
九年级人数 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 | 78.3 | 77.5 | 75 | 33.6 |
九年级 | 78 | 80.5 | a | 52.1 |
(1)表格中a的值为______;
(2)请你估计该校九年级体质健康优秀的学生人数为多少?
(3)根据以上信息,你认为哪个年级学生的体质健康情况更好一些?请说明理由.(请从两个不同的角度说明推断的合理性)