��Ŀ����
����Ŀ���ҹ��ж����������������������أ����������ѿ̲��ݻ�������ij�����̳��������ڽ�����Ҫ����������ij�ּ��ÿ������������������![]() Ԫ
Ԫ![]() ̨�����г����ۺ��֣���һ�����ڣ����ۼ���
̨�����г����ۺ��֣���һ�����ڣ����ۼ���![]() Ԫ
Ԫ![]() ̨ʱ�����۳�
̨ʱ�����۳�![]() ̨�����ۼ�ÿ����
̨�����ۼ�ÿ����![]() Ԫ���Ϳɶ��۳�
Ԫ���Ϳɶ��۳�![]() ̨���������̹涨���ֿ����������ۼ۲��ܵ���
̨���������̹涨���ֿ����������ۼ۲��ܵ���![]() Ԫ
Ԫ![]() ̨������������ÿ��Ҫ��ɲ�����
̨������������ÿ��Ҫ��ɲ�����![]() ̨����������
̨����������
��1����ȷ����������![]() ��̨�����ۼ�
��̨�����ۼ�![]() ��Ԫ
��Ԫ![]() ̨��֮��ĺ�����ϵʽ��
̨��֮��ĺ�����ϵʽ��
��2�����ۼ�![]() �ķ�Χ��
�ķ�Χ��
��3�����ۼ�![]() ��Ԫ
��Ԫ![]() ̨����Ϊ����ʱ���̳�ÿ���������ֿ�������������õ�����
̨����Ϊ����ʱ���̳�ÿ���������ֿ�������������õ�����![]() ��Ԫ�������������Ƕ��٣�
��Ԫ�������������Ƕ��٣�
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]()
��������
��1�����������������ۼ�ÿ����10Ԫ�����������Ϳɶ��۳�50̨�������г�������ϵʽ��
��2�����ݹ����̹涨���ֿ����������ۼ۲��ܵ���300Ԫ/̨������������ÿ��Ҫ��ɲ�����450̨�����ۼ������x��ȡֵ��
��3����x��ʾy��Ȼ������x����ʾ��w�����ݺ�����ϵʽ������������w.
�⣺��1���������![]() ����
����![]() ��
��
��2���������![]()
���![]() ��
��
��3��![]() ��
��
������![]() ��
��
![]() ��
��![]() ʱ�����ֵΪ
ʱ�����ֵΪ![]() ��
��
���ۼ�Ϊ![]() Ԫ
Ԫ![]() ̨ʱ��������������������Ϊ
̨ʱ��������������������Ϊ![]() Ԫ.
Ԫ.

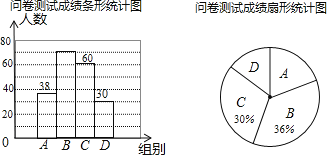
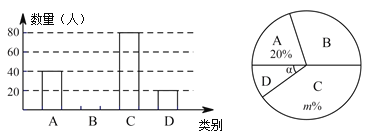
����Ŀ��Ϊ���˽�ͬѧ�Ƕ���������֪ʶ���˽�̶ȣ���ǿͬѧ�ǵĻ�����ʶijУ��ѧ��ȤС�����������������֪ʶ��Ͷ��������ʾ������ڱ�У�����ȡ������ͬѧ�������ʾ����ԣ����ݲ��Գɼ��ֲ�����������Գɼ��ֳ�A��B��C��D���飬����������ͳ��ͼ��
�ʾ����Գɼ������
��� | ����/�� |
A | 60��x��70 |
B | 70��x��80 |
C | 80��x��90 |
D | 90��x��100 |
��1������������������������ ����
��2�������У����Գɼ���B���Ƶ������ ����D���Ƶ������ ����
��3�������У���β��Գɼ�����λ�������� ���飻
��4�������У����880��ѧ��������Ƴɼ���90��x��100��ѧ��Լ���� ���ˣ�