题目内容
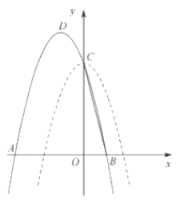
【题目】如图,将抛物线![]() 平移后,新抛物线经过原抛物线的顶点
平移后,新抛物线经过原抛物线的顶点![]() ,新抛物线与
,新抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,联结
,联结![]() ,
,![]() ,设新抛物线与
,设新抛物线与![]() 轴的另一交点是
轴的另一交点是![]() ,新抛物线的顶点是
,新抛物线的顶点是![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)设点![]() 在新抛物线上,联结
在新抛物线上,联结![]() ,如果
,如果![]() 平分
平分![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,将抛物线![]() 沿
沿![]() 轴左右平移,点
轴左右平移,点![]() 的对应点为
的对应点为![]() ,当
,当![]() 和
和![]() 相似时,请直接写出平移后得到抛物线的表达式.
相似时,请直接写出平移后得到抛物线的表达式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)设点D坐标(a,b),可得新抛物线解析式为:y=-![]() (x-a)2+b,先求出点C,点B坐标,代入解析式可求解;
(x-a)2+b,先求出点C,点B坐标,代入解析式可求解;
(2)通过证明△AOC∽△CHD,可得∠ACO=∠DCH,可证EC∥AO,可得点E纵坐标为4,即可求点E坐标;
(3)分两种情况讨论,由相似三角形的性质可求点F坐标,即可求平移后得到抛物线的表达式.
(1)∵抛物线y=-![]() x2+4的顶点为C,
x2+4的顶点为C,
∴点C(0,4)
∴OC=4,
∵tanB=4=![]() ,
,
∴OB=1,
∴点B(1,0)
设点D坐标(a,b)
∴新抛物线解析式为:y=-![]() (x-a)2+b,且过点C(0,4),点B(1,0)
(x-a)2+b,且过点C(0,4),点B(1,0)
∴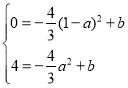
解得: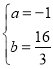
∴点D坐标(-1,![]() )
)
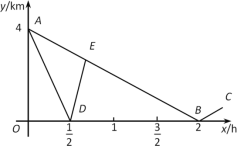
(2)如图1,过点D作DH⊥OC,
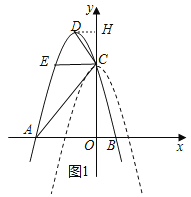
∵点D坐标(-1,![]() )
)
∴新抛物线解析式为:y=-![]() (x+1)2+
(x+1)2+![]() ,
,
当y=0时,0=-![]() (x+1)2+
(x+1)2+![]() ,
,
∴x1=-3,x2=1,
∴点A(-3,0),
∴AO=3,
∴![]() ,
,
∵点D坐标(-1,![]() )
)
∴DH=1,HO=![]() ,
,
∴CH=OH-OC=![]() ,
,
∴![]() ,
,
∴![]() ,且∠AOC=∠DHC=90°,
,且∠AOC=∠DHC=90°,
∴△AOC∽△CHD,
∴∠ACO=∠DCH,
∵CE平分∠ACD,
∴∠ACE=∠DCE,
∴∠ACO+∠ACE=∠DCH+∠DCE,且∠ACO+∠ACE+∠DCH+∠DCE=180°
∴∠ECO=∠ECH=90°=∠AOB,
∴EC∥AO,
∴点E纵坐标为4,
∴4=-![]() (x+1)2+
(x+1)2+![]() ,
,
∴x1=-2,x2=0,
∴点E(-2,4),
(3)如图2,
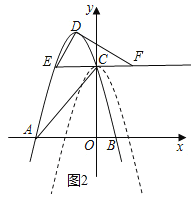
∵点E(-2,4),点C(0,4),点A(-3,0),点B(1,0),点D坐标(-1,![]() )
)
∴DE=DC=![]() ,
,![]() ,AB=3+1=4,
,AB=3+1=4,
∴∠DEC=∠DCE,
∵EC∥AB,
∴∠ECA=∠CAB,
∴∠DEC=∠CAB,
∵△DEF和△ABC相似
∴![]() 或
或![]() ,
,
∴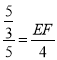 或
或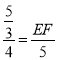
∴EF=![]() 或
或![]()
∴点F(-![]() ,4)或(
,4)或(![]() ,4)
,4)
设平移后解析式为:y=-![]() (x+1-c)2+4,
(x+1-c)2+4,
∴4=-![]() (-
(-![]() +1-c)2+4或4=-
+1-c)2+4或4=-![]() (
(![]() +1-c)2+4,
+1-c)2+4,
∴c1=![]() ,c2=
,c2=![]()
∴平移后解析式为:y=-![]() (x+
(x+![]() )2+4或y=-
)2+4或y=-![]() (x-
(x-![]() )2+4,
)2+4,

 一本好题口算题卡系列答案
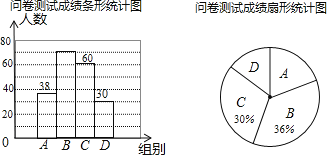
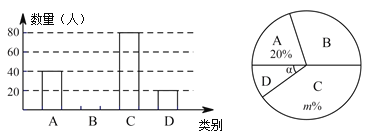
一本好题口算题卡系列答案【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表
问卷测试成绩分组表
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽样调查的样本总量是 ;
(2)样本中,测试成绩在B组的频数是 ,D组的频率是 ;
(3)样本中,这次测试成绩的中位数落在 组;
(4)如果该校共有880名学生,请估计成绩在90<x≤100的学生约有 人.