题目内容
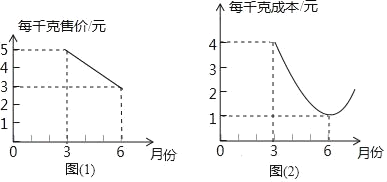
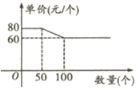
【题目】某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具,两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买![]() 个,如果甲、乙两商店分别购买玩具,两商店需付款总和为
个,如果甲、乙两商店分别购买玩具,两商店需付款总和为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱?
【答案】(1)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;(2)甲、乙两商店联合购买比分别购买最多可节约1840元.
;(2)甲、乙两商店联合购买比分别购买最多可节约1840元.
【解析】
(1)设玩具的单价为![]() 元,当
元,当![]() ,求出单价与数量的关系式,分段考虑:当
,求出单价与数量的关系式,分段考虑:当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ;(2)根据
;(2)根据![]()
![]()
![]() ,求函数最值,然后求出联合购买的钱数,比较即可.
,求函数最值,然后求出联合购买的钱数,比较即可.
(1)![]() 乙商店所需数量不超过50个,
乙商店所需数量不超过50个,
![]() ,解得
,解得![]() ,
,
![]() ,
,
设玩具的单价为![]() 元,
元,
当![]() ,设单价与数量的关系式为
,设单价与数量的关系式为![]() ,
,
由题意得![]() ,解得
,解得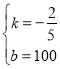 ,
,
![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
(2)![]()
![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() 最大值9040,
最大值9040,
![]() 最多节约的费用为
最多节约的费用为![]() 元,
元,
答:甲、乙两商店联合购买比分别购买最多可节约1840元.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系,关于销售单价,日销售量,日销售利润的几组对应值如表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | 25 |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y与x的函数关系式;
(2)当销售单价x为多少元时,日销售利润w最大?最大利润是多少元?
(3)当销售单价x为多少元时,日销售利润w在1500元以上?(请直接写出x的范围)