题目内容
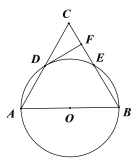
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2![]() ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为________.
,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为________.

【答案】![]() -1
-1
【解析】
如下图所示,由E点在以AD为直径的圆上,故由圆周角知道∠AED=90°,又B、E、D三点在一条直线上,∴∠AEB=180°-∠AED=90°,∴动点E点在以AB的中点O为圆心,AO为半径的圆上,故O、E、C三点共线时CE有最小值.
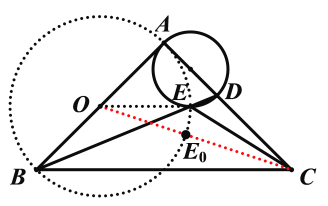
∵∠BAC=90°,AB=AC,且BC=![]() ,
,
∴AB=AC=2
∵AD为直径,E在AD为直径的圆上,∴∠AED为圆周角
由直径所对的圆周角为90°知:∠AED=90°
又∵B、E、D三点在一条直线上,∴∠AEB=180°-90°=90°
由90°所对的弦是直径知:
∴E点在以AB的中点O为圆心,AO为直径的圆上
故O、E、C三点共线时,即E在图中![]() 位置时,CE有最小值.
位置时,CE有最小值.
又OC=![]() ,
,
∴CE的最小值为![]()
故答案为:![]()

练习册系列答案
相关题目