题目内容
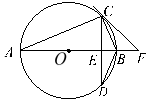
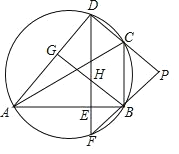
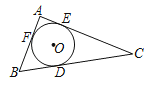
【题目】如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E.F.且AB=5,AC=12,BC=13,则⊙O的半径是_____.
【答案】2
【解析】
由题意根据勾股定理的逆定理可得三角形ABC为直角三角形,再根据切线长定理即可求解.
解: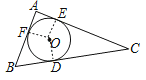
如图,连接OD、OE、OF,
∵△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E.F,
∴OE⊥AC,OF⊥AB,AE=AF,
∵AB=5,AC=12,BC=13,
即52+122=132,
∴△ABC为直角三角形,
∴∠A=90°,
∴四边形AEOF是正方形,
∴OE=OF=AE=AF,
设⊙O的半径是r,
则AF=AE=r,BF=BD=5﹣r,EC=DC=12﹣r,
∵BD+DC=BC=13,
∴5﹣r+12﹣r=13,
解得r=2.
所以⊙O的半径是2.
故答案为2.

练习册系列答案
相关题目
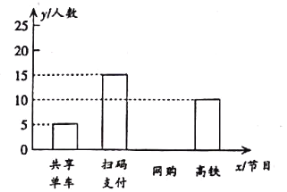
【题目】为了了解某小区青年对“高铁”、“扫码支付”、“网购”和“共享单车”新四大发明的喜爱程度,随机调查该小区一部分青年(每名青年只能选一个),并将调查结果制成如图所示统计表与条形统计图.
青年最喜爱的新四大发明人数统计表
节目 | 人数(名) | 百分比 |
共享单车 | 5 |
|
扫码支付 | 15 |
|
网购 |
|
|
高铁 | 10 |
|
青年最喜爱的新四大发明人数条形统计图
(1)计算![]() 的值
的值![]() ;
;
(2)请补全条形统计图;
(3)在被调查喜爱“共享单车”青年中,小明一周内使用共享单车的次数分别为:1,3,5,12,![]() ,若整数
,若整数![]() 是这组数据的中位数,直接写出该组数据的平均数.
是这组数据的中位数,直接写出该组数据的平均数.