题目内容
【题目】位于合肥滨湖新区的渡江战役纪念馆，实物图如图1所示，示意图如图2所示．某学校数学兴趣小组通过测量得知，纪念馆外轮廓斜坡AB的坡度i=1： 
，底基BC=50m，∠ACB=135°，求馆顶A离地面BC的距离．（结果精确到0.1m，参考数据： 
≈1.41， ≈1.73）
【答案】解：如解图，过点A作AD⊥BC交BC的延长线于点D．
∵∠ACB=135°，
∴△ADC为等腰直角三角形，
设AD=x，则CD=x，BD=50+x，
∵斜坡AB的坡度i=1：，
∴x：（50+x）=1：，
整理得（﹣1）x=50，
解得x=25（+1）≈68.3．
答：馆顶A离地面BC的距离约为68.3 m．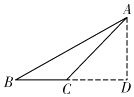
【解析】根据题干中给出的角，构造直角三角形．过点A作AD⊥BC交BC的延长线于点D，设AD=x，用x表示出CD、BD，再根据坡度i=1：，列出等量关系式即可得解．
【考点精析】关于本题考查的关于坡度坡角问题，需要了解坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA才能得出正确答案．
练习册系列答案
相关题目
