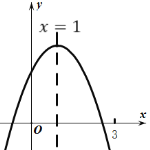ЬтФПФкШн
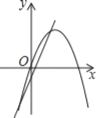
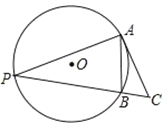
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() гыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
гыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
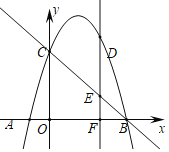
ЃЈ1ЃЉжБНгаДГіЕуAЁЂBЁЂCЕФзјБъЃЛ
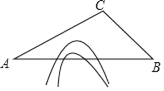
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯДцдквЛЕуPЃЌЪЙЕУPA+PCЕФжЕзюаЁЃЌЧѓДЫЪБЕуPЕФзјБъЃЛ
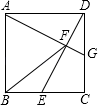
ЃЈ3ЃЉЕуDЪЧЕквЛЯѓЯоФкХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЈгыЕуCЁЂBВЛжиКЯЃЉЙ§ЕуDзїDFЁЭxжсгкЕуFЃЌНЛжБЯпBCгкЕуEЃЌСЌНгBDЃЌжБЯпBCАбЁїBDFЕФУцЛ§ЗжГЩСНВПЗжЃЌЪЙ![]() ЃЌЧыЧѓГіЕуDЕФзјБъЃЛ
ЃЌЧыЧѓГіЕуDЕФзјБъЃЛ
ЃЈ4ЃЉШєMЮЊХзЮяЯпЖдГЦжсЩЯвЛЖЏЕуЃЌЪЙЕУЁїMBCЮЊжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕуMЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЕуAЁЂBЁЂCЕФзјБъЗжБ№ЮЊЃКЃЈ1ЃЌ0ЃЉЁЂЃЈ5ЃЌ0ЃЉЁЂЃЈ0ЃЌ5ЃЉЃЛЃЈ2ЃЉPЃЈ2ЃЌ3ЃЉЃЛЃЈ3ЃЉDЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ4ЃЉMЕФзјБъЮЊЃКЃЈ2ЃЌ7ЃЉЛђЃЈ2ЃЌ3ЃЉЛђЃЈ2ЃЌ6ЃЉЛђЃЈ2ЃЌ1ЃЉЃЎ
ЃЉЃЛЃЈ4ЃЉMЕФзјБъЮЊЃКЃЈ2ЃЌ7ЃЉЛђЃЈ2ЃЌ3ЃЉЛђЃЈ2ЃЌ6ЃЉЛђЃЈ2ЃЌ1ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉСюyЃН0ЃЌдђxЃН1Лђ5ЃЌСюxЃН0ЃЌдђyЃН5ЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЕуBЪЧЕуAЙигкКЏЪ§ЖдГЦжсЕФЖдГЦЕуЃЌСЌНгBCНЛХзЮяЯпЖдГЦжсгкЕуPЃЌдђЕуPЮЊЫљЧѓЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉSЁїBDEЃКSЁїBEFЃН2ЃК3ЃЌдђ![]() ЃЌМДЃК
ЃЌМДЃК![]() ЃЌМДПЩЧѓНтЃЛ
ЃЌМДПЩЧѓНтЃЛ
ЃЈ4ЃЉЗжMBЮЊаББпЁЂMCЮЊаББпЁЂBCЮЊаББпШ§жжЧщПіЃЌЗжБ№ЧѓНтМДПЩЃЎ
ЃЈ1ЃЉСюyЃН0ЃЌдђxЃН1Лђ5ЃЌСюxЃН0ЃЌдђyЃН5ЃЌ
ЙЪЕуAЁЂBЁЂCЕФзјБъЗжБ№ЮЊЃКЃЈ1ЃЌ0ЃЉЁЂЃЈ5ЃЌ0ЃЉЁЂЃЈ0ЃЌ5ЃЉЃЛ
ЃЈ2ЃЉХзЮяЯпЕФЖдГЦжсЮЊЃКxЃН2ЃЌ
ЕуBЪЧЕуAЙигкКЏЪ§ЖдГЦжсЕФЖдГЦЕуЃЌСЌНгBCНЛХзЮяЯпЖдГЦжсгкЕуPЃЌдђЕуPЮЊЫљЧѓЃЌ
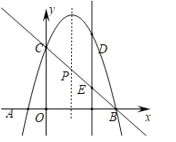
жБЯпBCЕФБэДяЪНЮЊЃКyЃНxЃЋ5ЃЌ
ЕБxЃН2ЪБЃЌyЃН3ЃЌЙЪЕуPЃЈ2ЃЌ3ЃЉЃЛ
ЃЈ3ЃЉЩшЕуDЃЈxЃЌx2ЃЋ4xЃЋ5ЃЉЃЌдђЕуEЃЈxЃЌxЃЋ5ЃЉЃЌ
ЁпSЁїBDEЃКSЁїBEFЃН2ЃК3ЃЌдђ![]() ЃЌ
ЃЌ
МДЃК![]() ЃЌ
ЃЌ
НтЕУЃКmЃН![]() Лђ5ЃЈЩсШЅ5ЃЉЃЌ
Лђ5ЃЈЩсШЅ5ЃЉЃЌ
ЙЪЕуDЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ4ЃЉЩшЕуMЃЈ2ЃЌmЃЉЃЌЖјЕуBЁЂCЕФзјБъЗжБ№ЮЊЃКЃЈ5ЃЌ0ЃЉЁЂЃЈ0ЃЌ5ЃЉЃЌ
дђMB2ЃН9ЃЋm2ЃЌMC2ЃН4ЃЋЃЈm5ЃЉ2ЃЌBC2ЃН50ЃЌ
ЂйЕБMBЮЊаББпЪБЃЌдђ9ЃЋm2ЃН4ЃЋЃЈm5ЃЉ2ЃЋ50ЃЌНтЕУЃКmЃН7ЃЛ
ЂкЕБMCЮЊаББпЪБЃЌдђ4ЃЋЃЈm5ЃЉ2=9ЃЋm2+50ЃЌПЩЕУЃКmЃН3ЃЛ
ЂлЕБBCЮЊаББпЪБЃЌдђ4ЃЋЃЈm5ЃЉ2+9ЃЋm2=50ПЩЕУЃКmЃН6Лђ1ЃЛ
злЩЯЕуMЕФзјБъЮЊЃКЃЈ2ЃЌ7ЃЉЛђЃЈ2ЃЌ3ЃЉЛђЃЈ2ЃЌ6ЃЉЛђЃЈ2ЃЌ1ЃЉЃЎ