题目内容
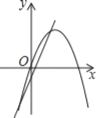
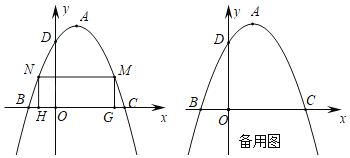
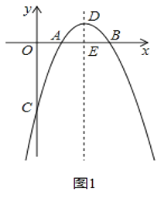
【题目】如图1，抛物线y＝ax2+bx﹣3与x轴交于A（1，0）、B两点，与y轴交于点C，抛物线的对称轴为直线x＝2，交抛物线于点D，交x轴于点E．
（1）请直接写出：抛物线的函数解析式及点B、点D的坐标；
（2）抛物线对称轴上的一动点P从点D出发，以每秒1个单位的速度向上运动，连接OP，BP，设运动时间为t秒（t＞0）．在点P的运动过程中，请求出：当t为何值时，∠OPB＝90°？
（3）如图2，点Q在抛物线上运动（点Q不与点A、B重合），当△QBC的面积与△ABC的面积相等时，请求出点Q的坐标．
【答案】（1）抛物线的表达式为：y＝﹣x2+4x﹣3；B（3，0），D（2，1）；（2）t＝
-1.
（3）（
，
）、（
、
）或（2，1）
【解析】
（1）根据待定系数法即可得到抛物线的表达式，再结合题意即可得到点B、点D的坐标；
（2）假设t秒时，点P（2，1+t），由题意可得OP2＝4+（1+t）2，BP2＝1+（1+t）2，AB2＝9，根据勾股定理可得4+（1+t）2+1+（1+t）2＝9，计算即可得到答案．
（3）根据题意算出点Q与BC的距离，求出与BC平行且距离为此距离的平行线的直线方程，与二次函数联立即可求解.
解：（1）抛物线y＝ax2+bx﹣3与x轴交于A（1，0），抛物线的对称轴为直线x＝2，则点B（3，0），
抛物线的表达式为：y＝a（x﹣1）（x﹣3）＝a（x2﹣4x+3），
即3a＝﹣3，解得：a＝﹣1，
故抛物线的表达式为：y＝﹣x2+4x﹣3…①，
函数的对称轴为：x＝2，则点D（2，1）；
（2）t秒时，点P（2，1+t），
则OP2＝4+（1+t）2，BP2＝1+（1+t）2，AB2＝9，
∵∠OPB＝90°，则4+（1+t）2+1+（1+t）2＝9，
解得：t＝-1（负值已舍去）．
（3）如下图，过点A作BC的平行线交抛物线于点Q、交y轴于点K，
则△QBC的面积与△ABC的面积相等，过点A作AG⊥BC于点G，过点K作KH⊥BC于点H，则AG＝KH，
直线BC的倾斜角为45°，则AG＝
AB＝＝KH，
则KC＝2，故点K（﹣1，0），[来源:.Com]
则直线AQ的函数表达式为：y＝x﹣1…②，
联立①②并解得：x＝1或2（舍去1），
故点Q（2，1）；
在BC的下方与AQ等距离位置作BC的抛物线交抛物线于点Q′、Q″，
同理可得直线Q′Q″的表达式为：y＝x﹣5…③，
联立①③并解得：x＝
，
故点Q（Q′、Q″）的坐标为：（，）、（、）；
综上，点Q的坐标为：（，）、（、）或（2，1）．
