题目内容
【题目】观察下列有规律的算式：13=1，13+23=9，13+23+33=36，13+23+33+43=100，13+23+33+43+53=225，…，探究并运用其规律计算：113+123+133+143+153+163+173+183+193+203的结果可表示为（ ）
A.
B.
C.
D.
【答案】A
【解析】
找出已知等式的运算规律，并归纳公式，然后先求出13+23+33+……+113+123+133+143+153+163+173+183+193+203的值，再求出13+23+33+……103的值，最后两式相减并利用平方差公式化简即可．
解：13=1，
13+23=9=（1+2）2，
13+23+33=36=（1+2+3）2，
13+23+33+43=100=（1+2+3+4）2，
13+23+33+43+53=225=（1+2+3+4+5）2，
∴13+23+33+……+n3=（1+2+3+……+n）2=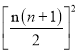
，
∴13+23+33+……+113+123+133+143+153+163+173+183+193+203=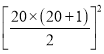
=2102①
而13+23+33+……103=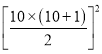
=552②
∴①－②，得
113+123+133+143+153+163+173+183+193+203=2102－552=（210＋55）×（210－55）=265×155
故选A．
【题目】某公司推出一款产品，经市场调查发现，该产品的日销售量y（个）与销售单价x（元）之间满足一次函数关系．关于销售单价，日销售量，日销售利润的几组对应值如下表：
销售单价x（元） | 85 | 95 | 105 | 115 |
日销售量y（个） | 175 | 125 | 75 | m |
日销售利润w（元） | 875 | 1875 | 1875 | 875 |
（注：日销售利润=日销售量×（销售单价﹣成本单价））
（1）求y关于x的函数解析式（不要求写出x的取值范围）及m的值；
（2）根据以上信息，填空：
该产品的成本单价是 元，当销售单价x= 元时，日销售利润w最大，最大值是 元；
（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？
【题目】某单位要将一份宣传资料进行批量印刷．在甲印刷厂，在收取100元制版费的基础上，每份收费0.5元；在乙印刷厂，在收取40元侧版费的基础上，每份收费0.7元．设该单位要印刷此宣传资料
份（为正整数）．
（Ⅰ）根据题意，填写下表：
印剧数量（份） | 150 | 250 | 350 | 450 | … |
甲印刷厂收费（元） | 175 | ① | 275 | ② | … |
乙印刷厂收费（元） | 145 | 215 | ③ | 355 | … |
（Ⅱ）设在甲印刷厂收费
元，在乙印刷厂收费
元，分别写出，关于的函数解析式；
（Ⅲ）当
时，在哪家印刷厂花费少？请说明理由．