题目内容
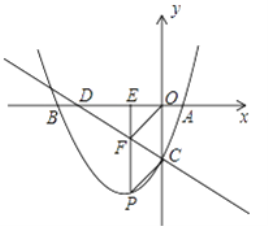
【题目】如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
(1)求D点的坐标和圆D的半径;
(2)求sin ∠ACB的值和经过C、A、B三点的抛物线对应的函数表达式;
(3)设抛物线的顶点为F,证明直线AF与圆D相切.
【答案】(1)点D的坐标为(5,4),圆的半径为5;(2)sin∠ACB=![]() ,y=
,y=![]() x2-
x2-![]() x+4;(3)详见解析.
x+4;(3)详见解析.
【解析】
(1)连接CD,过点D作DE⊥AB,垂足为E,连接AD.依据垂径定理可知AE=3,然后依据切线的性质可知CD⊥y轴,然后可证明四边形OCDE为矩形,则DE=4,然后依据勾股定理可求得AD的长,故此可求得⊙D的半径和点D的坐标;
(2)先求得A(2,0)、B(8,0).设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入可求得a的值.根据三角形面积公式得:S△ABC=![]() BC×ACsin∠ACB=
BC×ACsin∠ACB=![]() AB×CO,代入计算即可;
AB×CO,代入计算即可;
(3)求得抛物线的顶点F的坐标,然后求得DF和AF的长,依据勾股定理的逆定理可证明△DAF为直角三角形,则∠DAF=90°,故此AF是⊙D的切线.
(1)连接CD,过点D作DE⊥AB,垂足为E,连接AD.
∵DE⊥AB,∴AE![]() AB=3.
AB=3.
∵⊙D与y轴相切,∴DC⊥y轴.
∵∠COE=∠OED=∠OCD=90°,∴四边形OCDE为矩形,∴OC=DE.
∵C(0,4),∴DE=4.
在Rt△AED中,AD![]() 5,∴⊙D的半径为5,∴D(5,4).
5,∴⊙D的半径为5,∴D(5,4).
故答案为:(5,4),5.
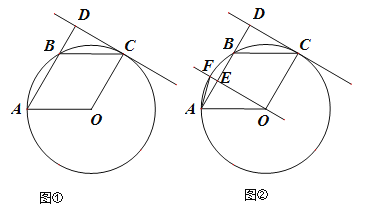
(2)如图1所示:
∵D(5,4),∴E(5,0),∴A(2,0)、B(8,0).
设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入得:16a=4,解得:a![]() ,∴抛物线的解析式为y
,∴抛物线的解析式为y![]() x2
x2![]() x+4.
x+4.
∵S△ABC=![]() BC×ACsin∠ACB=
BC×ACsin∠ACB=![]() AB×CO,∴sin∠ACB=
AB×CO,∴sin∠ACB=![]() =
=![]() .
.
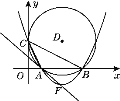
(3)连接DF,如图2.
∵y![]() x2
x2![]() x+4=
x+4=![]() ,∴抛物线的顶点坐标F(5,
,∴抛物线的顶点坐标F(5,![]() ),∴DF=4
),∴DF=4![]() ,AF
,AF![]() .
.
又∵AD=5,∴AD2+AF2=DF2,∴△DAF为直角三角形,∴∠DAF=90°,∴AF是⊙D的切线.

 阅读快车系列答案
阅读快车系列答案