题目内容
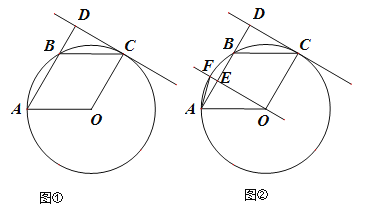
【题目】(本小题10分)已知A, B,C是⊙O上的三个点,四边形OABC是平行四边形,过点C作⊙O的切线,交AB的延长线于点D.
(Ⅰ)如图①,求∠ADC的大小;
(Ⅱ)如图②,经过点O作CD的平行线,与AB交于点E,与![]() 交于点F,连接AF,求∠FAB的大小.
交于点F,连接AF,求∠FAB的大小.
【答案】(Ⅰ)∠ADC=90°;(Ⅱ)∠FAB=15°.
【解析】
试题(Ⅰ)由切线的性质可得OC⊥CD,又由四边形OABC是平行四边形可得AD∥OC,即可求得∠ADC的度数.(Ⅱ)连接OB,易证△AOB是等边三角形;由OF∥CD可得∠AEO=∠ADC=90°;再根据垂径定理可得弧BF=弧AF,最后由圆周角定理即可求得∠FAB的度数.
试题解析:解:(Ⅰ)∵CD为⊙O的切线,C为切点,
∴OC⊥CD,即∠OCD=90°.
∵四边形OABC是平行四边形,
∴AB∥OC,即AD∥OC.
有∠ADC+∠OCD=180°,
∴∠ADC=180°-∠OCD=90°.
(Ⅱ)
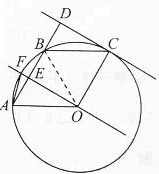
如图,连接OB,则OB=OA=OC.
∵四边形OABC是平行四边形,
∴OC=AB,
∴OA=OB=AB
即△AOB是等边三角形.
于是,∠AOB=60°.
由OF∥CD,又∠ADC=90°,
得∠AEO=∠ADC=90°.
∴OF⊥AB.有弧BF=弧AF.
∴∠FOB=∠FOA=![]() ∠AOB=30°.
∠AOB=30°.
∴∠FAB=![]() ∠FOB=15°.
∠FOB=15°.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目