Question

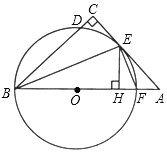
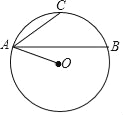
【题目】如图，已知AB是⊙O的弦，C是的中点，联结OA，AC，如果∠OAB＝20°，那么∠CAB的度数是_____．

Answer 1

【答案】35°

【解析】

连接CB，OB,CO，根据题意易得AC＝CB，再由等腰三角形三角形的性质、圆周角定理，进行角的代换计算即可得到答案.

连接CB，OB,CO.

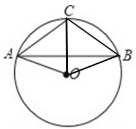
由题意＝ ,

∴AC＝CB,且△ABC是等腰三角形，∠CAO＝∠CBO

∵AO＝OB，在△AOB中

∴∠BAO＝∠ABO＝20°

∴∠AOB＝180°－∠BAO－∠ABO＝140°

∵AC＝CB

∴∠AOC＝∠BOC＝∠AOB＝70°

在△AOC中，AO＝CO，

∴∠CAO＝∠ACO＝（180°－70°）×＝55°

∴∠CAB＝∠CAO－∠OAB＝55°－20°＝35°

故答案为35°.